 I write a lot about the importance of confidence intervals and making the most of small sample sizes.
I write a lot about the importance of confidence intervals and making the most of small sample sizes.
Recently, Dean Barker, director of UX at Sage CRM read one of the articles on margins of error and sample sizes and said:
Math
Dean was referring to the fact that a completion rate from a sample of five users will have a 95% margin of error of approximately plus or minus 30 percentages points. For example, when one out of five users complete a task (20% completion rate), the 95% confidence interval is between 2% and 64%.
This means if we took 100 samples of five users from this population we’d expect the completion rate for all users to be between 2% and 64% around 95 times.
This wide confidence interval includes task completion rates that would be considered completely unusable to moderately usable (depending on the context).
Memory
After 20 years of experience and watching thousands of tasks in a lab, Dean said when he sees only a 20% completion rate at a sample of five, it’s pretty much the same when we he stops testing at 20. “I usually feel like I tested too many users not too few. Unusable tasks reveal themselves pretty early on.”
To test Dean’s experience with the math I created a simulator which tests thousands of completion rates at sample sizes of five and 20 against the actual completion rate at 10,000. You can simulate completion rates easily because they are limited to the range of (0 to 100%).
From the simulation we can see that completion rates on average only changes by about 10 percentage points between these a sample size of 5 and 20.
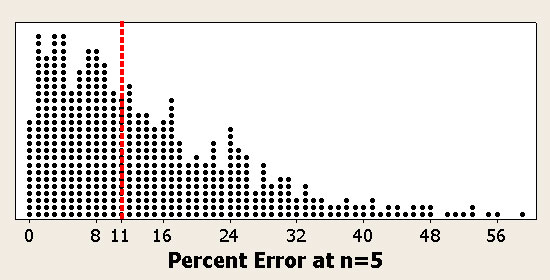 Interestingly enough, the average difference in completion rate at a sample of 5 and 10,000 only differs by around 11 percentage points!
Interestingly enough, the average difference in completion rate at a sample of 5 and 10,000 only differs by around 11 percentage points!
Dean’s seen something like 10,000 tasks in his career. In 5,000 of those tasks the completion rate will change less than 11 percentage points.
So if he sees a completion rate of 20% at five users, half the time the completion rate at 20 and 10,000 will between 9% and 29%.
Seventy-five percent of the time the completion rate will change by less than 21%. In other words, most of the time completion rates stay within a much narrower range—most tasks that are unusable really do look unusable at samples sizes of 5 and 20.
Reconciling Math and Memory
One of the misleading things about a 95% confidence interval is that the actual completion rate is much more likely to be in the middle than near the end-points. That is, the actual completion rate is much more likely to be say 30% than say 60% when you see only one out of five users succeed.
A way to think about a confidence interval is like looking at a spiral galaxy from the side. Most of the stars are clustered in the middle. Only a few are far out in the edges of the spirals.

If we drew a line where 95% of the stars would fall the line would need to be far out near the edges of the galaxy.
The same concept applies to confidence intervals.
The actual completion rate is most likely near the value you observed, even at a sample size of five.
If you need to be really sure you know where the completion rate will be (95 percent means really sure) then you have a wide interval.
This speaks to why you don’t always need such a high level of confidence in applied research. A 95% confidence interval contains many improbable events. In some cases you just have to be this sure as these improbable events can lead to major losses. In other cases you can sleep well knowing that there’s only a 20% chance the completion rate will exceed 41%.
Confidence intervals, like statistics in general, are powerful because they are both consistent with our experience and provide a level of precision we can’t articulate. You should use them with your usability test data. If you’re new to confidence intervals and quantifying usability data check out the popular Quantitative Starter Package.


