 Ask your customers if they’d recommend your product using a scale from 0 to 10 where 10 means extremely likely.
Ask your customers if they’d recommend your product using a scale from 0 to 10 where 10 means extremely likely.
Now find the average of the responses. Is an average score of say 7.212 good?
It’s hard to say.
Interpreting averages from rating scales is notoriously difficult unless you have something to compare the average to.
One of the reasons the Net Promoter Score is so popular is that it generates a seemingly more interpretable measure.
Net Promoter scoring segments the responses into three buckets.
Promoters: Responses from 9-10
Passives: Responses from 7-8
Detractors: Responses from 0 to 6
Then subtract the proportion of detractor responses from the proportion of promoter responses you get the Net Promoter Score.
Knowing that you have 20% more customers promoting than detracting your product does mean something. Of course, it still begs the question: is 20% good?
So you still need an industry benchmark to make sense of your Net Promoter Score. For example, the Consumer Software Industry has an average Net Promoter score of 21%–meaning a 20% is about average for products like Quicken, QuickBooks, Excel, Photoshop and iTunes. A 20% in the commercial Airlines industry would probably be among the highest scorers.
There are many ways to report the scores of rating scales, such as top-box scoring like the Net Promoter. We get some sense of intuitiveness, but how much do we lose in the process and would the mean work just as well?
Regression Analysis of Means and Net Promoter Scores
I looked at the Net Promoter Scores for 87 software products and large traffic websites. The sample sizes were between 30 and 300 and were collected over the past 12 months. There was a good range of low and high scores. I looked at the correlation between the mean response to the likelihood to recommend question and the properly computed Net Promoter Score.
I found that there was an extremely high correlation between the two (r = .959). In examining the relationship in the scatterplot you can see some curvature to the relationship and I found a cubic equation fit better than a linear one.
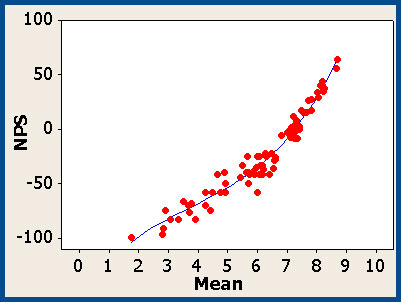
Figure 1: Relationship between the Mean and Net Promoter Score from 87 products and websites.
The regression equation is NPS = – 1.55 + 0.39*Mean – .07*Mean2 + .006 Mean3 [Adj-R2=96%]
What I found was the mean to the likelihood to recommend question can predict around 96% of the variability of the Net Promoter Score. That means there’s a loss of about 4% when converting between the mean and Net Promoter Score.
When you convert the 11 point scale to 3 points (Promoter, Passive and Detractor) you lose information. For example, if people switch scores from say 0’s to 5’s between products, there won’t be any change in the Net Promoter Score.
This analysis suggests you’re losing about 4% of the information when you use the Net Promoter Score instead of the mean.The graph and regression equation also show that a mean of about a 7.28 gets you a 0% NPS (the same proportion of Promoters and Detractors).
I’ve created two calculators below which will allow you to easily convert from a Net Promoter Score to a mean and from a mean to a Net Promoter Score.
Mean and Net Promoter Score Converter
Enter a mean to get an estimated Net Promoter Score or enter an NPS to get the estimated mean.
In short, using Net Promoter Scoring provides a possibly more digestible metric without suffering too much loss. The mean is a close substitute which may work better for statistical comparisons because it doesn’t lose any response information. Keep in mind, you’ll still want to compare your NPS to something meaningful like a competing product, prior release or industry benchmark.


