 Responses to rating-scale data typically don’t follow a normal distribution.
Responses to rating-scale data typically don’t follow a normal distribution.
However, this is unlikely to affect the accuracy of statistical calculations because the distribution of error in the measurement is normally distributed.
Top-box scoring of rating-scale data can provide an easy way to summarize or segment your data in the absence of a benchmark or comparison test.
Another reason top-box scores are used with rating-scale data like the Net Promoter Score is that there is a concern that the data are not normally distributed and thus make statistical calculations inaccurate.
By reporting on just the frequencies for each response you avoid problems with assumptions about normality. Unfortunately, condensing 11 responses into 2 or 3 sacrifices important information about precision and variability.
There will always be value in segmenting responses into groups for concise reporting (especially to executives). But when you want to determine whether your score has statistically improved, you’ll want to use the mean and standard deviation because they provide more precision at smaller sample sizes. Doing so means that you need to consider the distribution of your data.
What It Means To Be Normal
Even if you know enough about statistics to be dangerous, you’ve probably heard the warning that you need to be sure your data are normally distributed.
Fortunately, you don’t need to sit through a semester of statistics to understand the role of the normal distribution in analyzing rating-scale data like the question used to compute Net Promoter Scores.
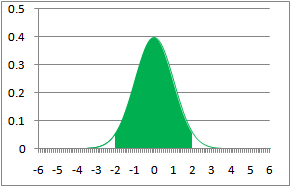
A normal distribution (sometimes called Gaussian just to confuse people) refers to data that, when graphed, “distributes” in a symmetrical bell shape with the bulk of the values falling close to the middle.
Normal distributions can be found everywhere: height, weight and IQ scores form some of the more famous normal distributions.The chart below shows the distribution of the heights of 500 North American men.
You can see the characteristic bell shape. The bulk of values fall close to the average height of 5’10” (178 cm) and roughly the same proportion of men are taller or shorter than average.
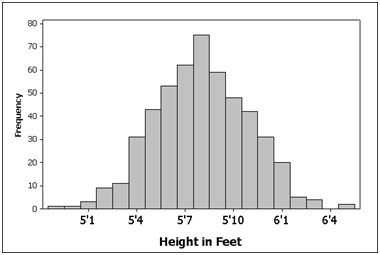
Figure 1: Distribution of heights of 500 men from North America. The apostrophe: (e.g. 5′) means feet.
Net Promoter Data Don’t Look Normal
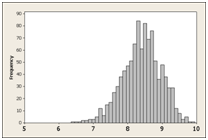
The popular Net Promoter Score measures customer loyalty using the following question: “How likely are you to recommend a product to a friend?” with responses on an 11-point rating-scale.
Here is the graph of the 673 responses to the “likelihood to recommend” question for a consumer software product. The mean response is 8.4 with a standard deviation of 1.8.
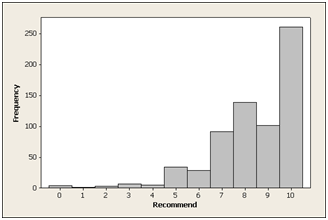
Figure 2: Distribution of 673 responses to the “Likelihood to Recommend” question for a consumer software product.
The graph hardly looks like a bell and certainly isn’t symmetric. It’s no wonder researchers have concerns using common statistical techniques like confidence intervals, t-tests or even the mean and standard deviation. When they see non-normal data like this they run!
Why Normality is Important
Normality is important for two reasons:
- Statistical tests assume the error in our measurement is normally distributed.
- We can’t speak accurately about the percentage of responses above and below the mean if our data is not normal.
Error in Measurement
By error in measurement I’m not talking about the kind that happens when someone misunderstands a question or miscodes the data from a survey. I’m talking about the unsystematic kind that comes from any sample.
When we calculate the mean from a sample, it estimates the unknown population mean. It is almost surely off—over or under—by some amount.
The difference between our sample mean and population mean is called sampling error, and it forms its own distribution. We want this distribution to be normal. If our sample of data is normal, then the distribution of sample means (the sampling error) is also normal.
Unfortunately, almost all rating scale data is not normal, so we need to examine the distribution of sample means. But how can we know what this distribution of all sample means looks like if we have only one sample mean?
If we had a lot of time on our hands, we could randomly ask 30 people if they’d recommend the product to a friend. We’d find the mean, graph it, and then rinse and repeat a million times. Or we could simulate that exercise by taking a lot of smaller random samples from a larger sample of data and using a few lines of code.
I chose the latter approach.
The Distribution of Sample Means
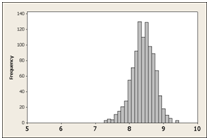
I took the large sample of 673 responses and wrote a short program which sampled random responses and computed the mean. I did this at sample sizes of 30, 10 and 5 and repeated it 1000 times for each sample size. The graphs of each distribution of sample means are shown below.
 |
 |
 |
| n=30 | n=10 | n=5 |
The distribution of 1000 means at sample sizes of 30 and 10 are bell-shaped, symmetrical and normal. The distribution at a sample size of 10 is a bit wider because smaller sample sizes have more variability.
At the sample size of 5, the distribution has less symmetry and a bit of a negative skew (more values in the lower scores). We have evidence that our sampling error deviates from normality.
Technical Note: Some normality tests generate p-values. These tend to be overly sensitive to minor deviations from normality and are not recommended. Looking at the data in a normal probability plot (also called a Q-Q plot) provides the most reliable assessment of normality. I used histograms here since it is easier to recognize the famous bell-shape.
The Central Limit Theorem
What we’re seeing in action is something called the Central Limit Theorem. It is the most important concept in statistics. It basically says that the distribution of sample means will be normal regardless of how ugly and non-normal your population data is, especially when the sample size is above 30 or so.
As we can see from my re-sampling exercise, the Central Limit Theorem often kicks-in at sample sizes much smaller than 30 (the sample of 10 is basically normal). Exactly how normal the data appear, and at what sample size, will depend on the data you have.
Fortunately, you don’t have to code a software program to know if your sampling distribution is normal (like you needed another reason not use statistics).
Even when sampling distributions are not normal for small sample sizes (less than 10), statistical tests like confidence intervals, t-tests and ANOVA still perform quite well. When they are inaccurate, the typical error is only a manageable 1% to 2% [ See GEP Box (1953) Non-normality and test on variance. Biometrika, 40 ].
In other words, when you think you’re computing a 95% confidence interval, it might be only a 94% confidence interval.
In short, for rating scale data from larger sample sizes (above 30) don’t worry about normality. For smaller samples sizes (especially below 10) you will find a modest and manageable amount of error in most statistical calculations.
Population Distribution
While the shape of your sample data probably doesn’t affect the accuracy of statistical tests, it does affect statements about what percent of the population scores fall above or below the average or other points.
For example, a statement such as “We can be 95% sure half of all users rate their likelihood to recommend above the average score of 8.4.” Using the mean to generate statements like this assume the data are symmetrical and roughly normal. We can see from the graph of the responses above that this is not the case. This is the same problem you run into with task-time data which is also non-normal.
With rating scale data the solution is easy. If you want to make statements about the percent of users that score above a certain score, then just count the discrete responses. For example, 362 of the 673 users (54%) provided scores of 9 or 10 (these users are classified as Promoters). Using a binomial confidence interval we can be 95% between 50% and 58% of all users are Promoters.
Another alternative is to transform the scores so that they follow a normal distribution. This is also the corrective procedure done when working with task-time data. With transformed data that are normally distributed even these percentage statements are accurate.
Normality Summary
In summary, normality should not be a concern for large sample sizes (above 30). For smaller sample sizes, the distribution of errors is probably normal or close to normal. When the data do depart from normality, most statistical tests still generate reliable and accurate results.
Normality is a concern when making statements about percentages of the population that score above or below certain values. In such situations, using the response frequencies or transforming the data are appropriate alternatives.
While I’ve only shown examples of responses to the “likelihood to recommend” question, the concept applies to all rating-scale data (like the System Usability Scale or Single Ease Question ).
My suggestion is to worry less about the normality of your data and worry more about the representativeness of it. That is, be sure your sample is representative of the population you’re making inferences about.
Whatever inaccuracies result from non-normal data are dwarfed by drawing the right conclusions about the wrong people. No statistical manipulations can account for an unrepresentative sample.
See the Crash Course in zScores if you want to learn more about the normal distribution or brush up on its critical role in statistics.
Editorial services courtesy of Marcia Riefer Johnston. See her “Word Power” blog.


