How many users will complete the task and how long will it take them? If you need to benchmark an interface, then a summative usability test is one way to answer these questions. Summative tests are the gold-standard for usability measurement. But just how precise are the metrics?
Just as a presidential poll uses a sample to estimate outcomes for the entire population, usability tests also estimate the population task time and completion rate from a sample of users. Also like presidential polls, our sample estimates won’t be exactly like the entire population. Instead, the estimates have a margin of error. If we were to sample 20 users, compute the mean time and completion rate, it would differ by some amount from the real average time and completion rate.
The margin of error is half the width of the confidence interval and the confidence interval tells us the likely range the population mean and proportion will fall in. Most presidential polls have a margin or error between +/- 3% and +/-5%. That means if they sampled another set of likely voters, the proportion saying they would vote a certain way would be expected to fluctuate between 6 and 10%. So what is the typical margin of error in a usability test?
To find out, I examined a large set of data from an earlier analysis Jim Lewis and I conducted. We collected data from 100 summative usability tests across a dozen companies taking place over the last 25 years. In total there is data from over 2000 users and 1000 tasks. The majority of sample sizes across the 1000 tasks were between 8 and 12 users (64%). Eighty percent of the tasks had less than 20 users. For each task I computed the confidence intervals then halved the confidence interval to generate the margin of error around the average task times and completion rate. For task time I excluded users who failed the task. The results are shown in the graph below.
Margin of Error for Task Times
Figure 1 below shows the 95% confidence interval around the average margin of error for each sample size. The margin of error was calculating by transforming the raw times using the natural log and computing a t-confidence interval. For example, at a sample size of 10, the average margin of error is between 34 and 38% of the mean. So if you had 10 users complete a task and you observed a mean time of 100 seconds, the mean of the entire population will likely be between 66 seconds and 134 seconds. Put another way, if you were to test another 10 users on the same task, their average time would most likely fall between 66 and 134 seconds.
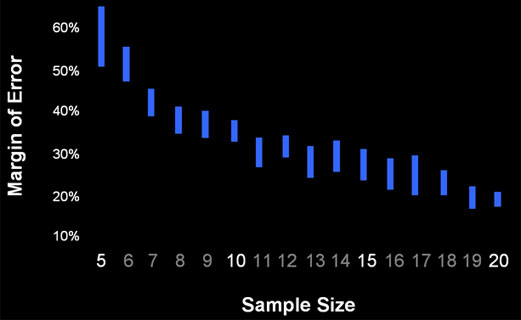
Figure 1: The 95% confidence interval around the average margin of error from 707 summative usability tasks by sample size.
The width of each blue-bar in Figure 1 above comes from the number of tasks at each sample size and the different variation for each task. With more variability and fewer sample tasks, the intervals get wider. The number of tasks and range of the 95% interval around the margin of error can be seen in the table below.
| Users | N(tasks) | Mean | Low | High |
|---|---|---|---|---|
On average, a sample of 10 will have a margin of error of +/-36%. For a task with a sample size of 20, there are 25 tasks and 95% of the margins of error fall between 17% and 21%. The typical margin of error at a sample size of 20 is approximately 20%.
The relationship between the sample size and the margin of error is an inverse square root relationship. That means if you want to cut your margin of error in half, you need to quadruple your sample size. If you have a sample size of 20 (with a typical margin of error of approximately 20%) and wanted a margin of error of 10%, you’d need to plan on testing approximately 80 users.
Margin of Error for Task Completion Rates
For margins of error around task completion rates we don’t need to examine a dataset, we can compute them for the sample sizes since there is a limited range in which a completion rate can fall (between 0% and 1%). The only unknown factor that would affect the margin of error is how close the completion rate is to 50%–the closer to 50%, the wider the margin of error (the adjusted-wald confidence interval was computed). I computed the margin of error using a completion rate of 50% and one at 95% (say for a production quality ecommerce site). The results are shown in the Figure 2 below.
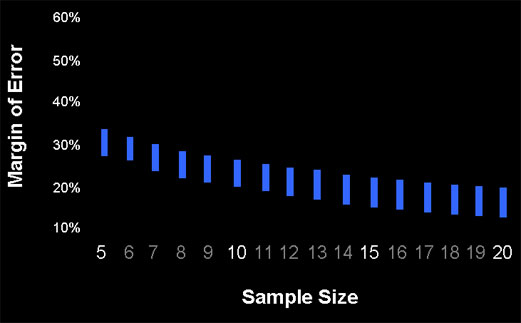
The upper portion of the bar shows the margin of error when the completion rate is 50% and the lower portion when the completion rate is 95%. There is on average about a six percentage point reduction in the width of the margin of error for the high completion rate of 95%.
| Users | 50% | 95% |
|---|---|---|
For example, at a sample size of 10, the margin of error will be approximately 26% for the completion rate of 50% and 20% for the 95% completion rate. At a sample size of 20, the margin of error is 20% for the 50% completion rate and 13% for the 95% completion rate. You should only plan your sample size around the 95% completion rate if you have strong evidence to indicate you’d observe a very high completion rate. Also note that the width of the margin of error is symmetrical around 50%, meaning a 75% completion rate generates the same margin of error as a 25% completion rate. Let’s hope the latter is not production software!
We again see an inverse square root pattern between the sample size and margin of error, similar to that for task time. Because the formula for confidence intervals use the inverse of the square root of the sample size, it isn’t much of a surprise.
If we are able to conduct a remote unmoderated usability test we can see what would happen to our precision with the increased sample sizes. The dataset we have contains 29 tasks that had more than 100 users who successfully completed the task.
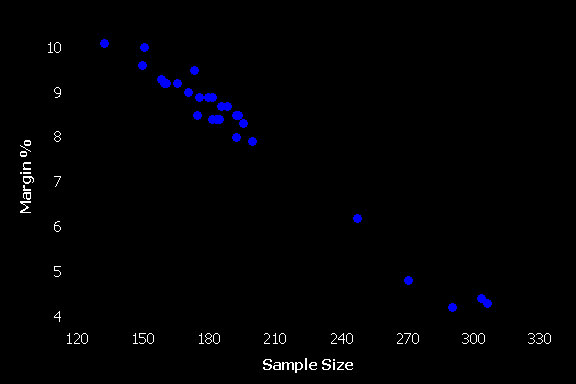
Figure 3: The margin of error for 29 task from remote unmoderated usability tests with sample sizes above 100.
In the figure above, each dot represents only 1 task, so it is at best a crude estimate of the expected margin of error for task times (the task time graph above has between 10 and 110 tasks for each sample size). It does given us one example to check the math predictions. For example, earlier I said that for a margin of error of 10% you should plan on around 80 users. We see that for a few tasks with 130 to 160 users, the margin of error is still as much as 10%. That’s because of higher than average variability with these tasks. Conversely, I said you’d need to have approximately a sample size of 320 to have a margin of error of 5%. We can see that level of precision is achieved with as few as 270 to 300 users for some tasks (not far off 320 though). There is less than average variability in the task times for these tasks.
To estimate task times, another alternative is to conduct a Keystroke Level Modeling analysis (remember GOMS ?). The research shows you can predict the task times for skilled users to with an accuracy of around 10% (the same level of precision as a usability test with 80 users). For a slight enhancement of the KLM method, see the paper on Composite Operators for Keystroke Level Modeling. .
We can take away from this analysis some simple rules of thumb for knowing the amount of precision in a usability test. Start with the 20/20 rule. At a sample size of 20, you’ll have a margin of error of around 20% (for both task times and completion rates). To cut the margin of error in half you need to quadruple the sample size. A margin of error of 10% would require around 80 users. The typical summative usability test with a sample size of around 10 has a margin of error close to +/-30%! To achieve a margin of error of 5%, you’d need a sample size of approximately 320.
Using the 20/20 rule will get you reasonably close to the precise number of users needed. For completion rates it will be very accurate because the values are confined between 0 and 1. For task times the variability has no theoretical upper limit, but the empirical data examined from 1000 tasks suggests the standard deviation is usually rather high (approximately half the mean), so the estimates of sample size using the 20/20 rule will also be close for task times—assuming you’re examining initial use and not practiced, skilled behavior. The margins of error analyzed from this dataset are also consistent with the earlier analysis by Nielsen, so there is corroborating evidence for high-variability in task times and their corresponding wide margins of errors.
Next time you’re conducting a lab based usability test, set your expectations for how precise your metrics will be (+/- 10-30%). Remember the 20/20 rule—at sample sizes of 20 you’ll have a margin of error of 20%. To achieve half that margin of error you’d need a sample size of 80. To achieve a margin of error of 5% you’ll need 320 users.


