 Most people are comfortable with the concept of an average or percentage as a measure of quality.
Most people are comfortable with the concept of an average or percentage as a measure of quality.
An equally important component of measuring the user experience is to understand variability.
Here are 10 things to know about measuring variability in the user experience.
- Variability is inherent to measuring human performance. People have different browsing patterns, speeds, inclinations and motivations when they use software or websites. Differences in prior experience and domain knowledge often play a primary role in how users solve problems and accomplish tasks in interfaces. This can lead to vastly different experiences–including encountering different interface problems and resulting in large differences in task performance times or perception metrics.
- Often the differences between users outweighs the differences between designs. One consequence of the high variability between users is that even major design changes aren’t detected in completion rates or perception metrics from observing samples of users. It might be that changes did make an impact, but the variability between users masks the findings.
- Two ways to manage high variability are increasing the sample size and using a within-subjects study. When making a comparison between designs, if each user attempts tasks on both designs (in a counterbalanced order), you effectively eliminate the between user variability. This is called a within-subjects study. Each user acts as their own control and differences between designs are easier to detect–even with small sample sizes.If you cannot use a within-subjects study or are not making a comparison, the next best alternative is to increase your sample size. Remember though that you need to roughly quadruple your sample size in order to cut your margin or error in half.
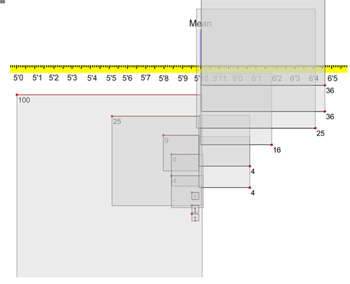
- The standard deviation is the most common measure of variability. While the mean describes the middle or most typical value, the standard deviation describes how far each value is from the mean. You can think of the standard deviation as the average difference each value is from the mean. The short tutorial below provides a visualization of the standard deviation using the heights of 14 men. It’s part of the full course Practical Statistics for UX and Customer Research.
- To compute the standard deviation in Excel use the formula =STDEV() or =STDEV.S() for measuring the sample standard deviation. You can also use an online calculator and see how to compute it by hand for those looking for some arithmetic exercises.
- The standard deviation is one of the three critical ingredients needed to compute a confidence interval and compare two means. The other two ingredients are the mean and sample size. That’s why journals will request authors provide these values so readers can replicate many findings just from these summary statistics. Oh and the standard deviation is also needed to compute effect sizes–which help you better interpret the size of differences and something journals really like to see.
- Standard deviations are used to measure the variability in findability times : Standard deviations can be difficult to interpret by themselves. One technique is to divide the standard deviation by the mean time and multiply the value by 100. This is called the coefficient of variation (CV). Smaller values indicate a less variable experience and longer CV’s mean a more variable experience. Anything over 100% is especially variable and worth investigating more. For example, a standard deviation of 110 divided by the mean of 100 seconds is a CV of 110%.
- For measuring task-times the average coefficient of variation is 44%: Task time data is positively skewed and the standard deviation is correlated with the mean time. While this can be a bad thing for working with many statistical procedures, it does allow us to predict standard deviations from mean times alone. Across hundreds of tasks we noticed the standard deviation is approximately 44% of the mean time. For example, if it takes users 50 seconds to find an item in a website navigation, a good guess at the standard deviation is 22 seconds.
- For binary data the standard deviation is derived from the proportion. The standard deviation is equal to the square root of the proportion times 1-proportion. A proportion has its highest variability at .5 and it decreases as you get closer to 0 or 1. While it might sound counter-intuitive, think of flipping a coin. There’s always a 50/50 chance of landing on tails, it’s the most variable as the outcome can be either heads or tails. Contrast that with playing the lottery where the proportion of winning is well less than .0001. For each ticket, the outcome will almost always be a non-winning ticket–a less variable and less profitable experience.
- The Standard deviation is used to compute sample sizes. It’s usually the case that researchers don’t have the standard deviation when computing sample sizes. Fortunately there are some work-arounds. For comparing task-time data, use 44% of the mean as a working estimate. For example, the sample size needed to detect a 20 second reduction in task times (from 110 seconds to 90 seconds) is around 124 people (62 in each group).Because the standard deviation is part of a proportion, you can also compute the sample size needed for comparing two proportions and apply it to comparing two means (like two rating scales). For example, the sample size needed to detect a 12 percentage point difference is 426 participants (213 in each group). Comparing means requires a smaller sample size than comparing proportions so you know the target sample size is smaller than 426. See chapter 6 in Quantifying the User Experience for computation examples and discussion.


