UX research and UX measurement can be seen as an extension of experimental design. At the heart of experimental design lie variables.
UX research and UX measurement can be seen as an extension of experimental design. At the heart of experimental design lie variables.
Earlier we wrote about different kinds of variables. In short, dependent variables are what you get (outcomes), independent variables are what you set, and extraneous variables are what you can’t forget (to account for).
When you measure a user experience using metrics—for example, the SUPR-Q, SUS, SEQ, or completion rate—and conclude that one website or product design is good, how do you know it’s really the design that is good and not something else? While it could be due to the design, it could also be that extraneous (or nuisance) variables, such as prior experiences, brand attitudes, and recruiting practices, are confounding your findings.
A critical skill when reviewing UX research findings and published research is the ability to identify when the experimental design is confounded.
Confounding can happen when there are variables in play that the design does not control and can also happen when there is insufficient control of an independent variable.
There are numerous strategies for dealing with confounding that are outside the scope of this article. In fact, it’s a topic that covers several years of graduate work in disciplines such as experimental psychology.
Our goal in this first of a series of articles is to show how to identify a specific type of confounded design in published experiments and demonstrate how their data can be reinterpreted once you’ve identified the confounding.
Incomplete Factorial Designs
One of the great scientific innovations in the early 20th century was the development of the analysis of variance (ANOVA) and its use in analyzing factorial designs. A full factorial design is one that includes multiple independent variables (factors), with experimental conditions set up to obtain measurements under each combination of levels of factors. This approach allows experimenters to estimate the significance of each factor individually (main effects) and see how the different levels of the factors might behave differently in combination (interactions). This is all great when the factorial design is complete, but when it’s incomplete, it becomes impossible to untangle potential interactions among the factors.
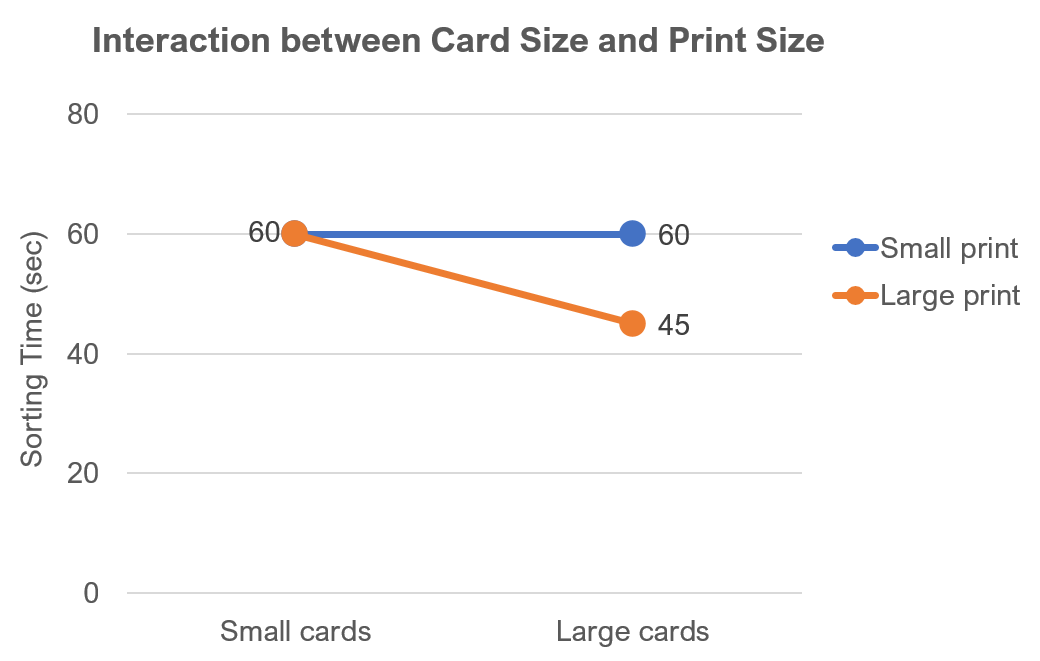
For example, imagine an experiment in which participants sort cards and there are two independent variables—the size of the cards (small and large) and the size of the print on the cards (small and large). This is the simplest full factorial experiment, having two independent variables (card size and print size), each with two levels (small and large). For this 2×2 factorial experiment, there are four experimental conditions:
- Large cards, large print
- Large cards, small print
- Small cards, large print
- Small cards, small print
The graph below shows hypothetical results for this imaginary experiment. There is an interaction such that the combination of large cards and large print led to a faster sort time (45 s), but all the other conditions have the same sort time (60 s).
But what if for some reason the experimenter had not collected data for the small card/small print condition? If you averaged across card size, you’d get the same average as you would collapsing the data over print size, which would be (60+45)/2 = 52.5. An experimenter focused on the effect of print size might claim that the data show a benefit to larger prints, but the counterargument would be that the effect is due to card size instead. With this incomplete design, you couldn’t say with certainty whether the benefit in the large card/large print condition was due to card size, print size, or that specific combination.
Moving from hypothetical to published experiments, we first show confounding in a famous psychological study, then in a somewhat less famous but influential human factors study, and finally in UX measurement research.
Harry Harlow’s Monkeys and Surrogate Mothers
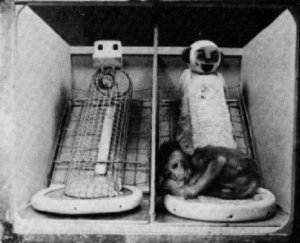
In the late 1950s and early 1960s, psychologist Harry Harlow conducted a series of studies with infant rhesus monkeys, most of which would be considered unethical by modern standards. In his most famous study, infant monkeys were removed from their mothers and given access to two surrogate mothers, one made of terry cloth (providing tactile comfort but no food) and one made of wire with a milk bottle (providing food but no tactile comfort). The key finding was that the infant monkeys preferred to spend more time close to the terry cloth mother, using the wire mother only to feed. The image below shows both mothers.
Image from Wikipedia.
In addition to the manipulation of comfort and food, there was also a clear manipulation of the surrogate mothers’ faces. The terry cloth mother’s face was rounded and had ears, nose, big eyes, and a smile. The wire mother’s face was square and devoid of potentially friendly features. With this lack of control, it’s possible that the infants’ preference for the terry cloth mother might have been due to just tactile comfort, just the friendly face, or a combination of the two. In addition to ethical issues associated with traumatizing infant monkeys, the experiment was deeply confounded.
Split Versus Standard Keyboards
Typing keyboards have been around for over 100 years, and there has been a lot of research on their design—different types of keys, different key layouts, and from the 1960s through the 1990s, different keyboard configurations. Specifically, researchers conducted studies of different types of split keyboards intended to make typing more comfortable and efficient by allowing a more natural wrist posture. The first design of a split keyboard was the Klockenberg keyboard, described in his 1926 book.
One of the most influential papers promoting split keyboards was “Studies on Ergonomically Designed Alphanumeric Keyboards” by Nakaseko et al., published in 1985 in the journal Human Factors. In that study, they described an experiment in which participants used three different keyboards—a split keyboard with a large wrist rest (see the figure below), a split keyboard with a small wrist rest, and a standard keyboard with a large wrist rest. They did not provide a rationale for failing to include a standard keyboard with a small wrist rest, and this omission made their experiment an incomplete factorial.
Image from Lewis et al. (1997) “Keys and Keyboards.”
They had participants rank the keyboards by preference, with the following results:
| Rank | Split with Large Rest | Split with Small Rest | Standard with Large Rest |
|---|---|---|---|
| 1 | 16 | 7 | 9 |
| 2 | 6 | 13 | 11 |
| 3 | 9 | 11 | 11 |
The researchers’ primary conclusion was “After the typing tasks, about two-thirds of the subjects asserted that they preferred the split keyboard models.” This is true because 23/32 participants’ first choice was a split keyboard condition. What they failed to note was that 25/32 participants’ first choice was a keyboard condition that included a large wrist rest. If they had collected data for with a standard keyboard and small wrist rest, it would have been possible to untangle the potential interaction—but they didn’t.
Effects of Verbal Labeling and Branching in Surveys
In recent articles, we explored the effect of verbal labeling of rating scale response options; specifically, whether partial or full labeling affects the magnitude of responses, first in a literature review, and then in a designed experiment.
One of the papers in our literature review was Krosnick and Berent (1993) [pdf]. They reported the results of a series of political science studies investigating the effects of full versus partial labeling of response options and branching. In the Branching condition, questions were split into two parts, with the first part capturing the direction of the response (e.g., “Are you a Republican, Democrat, or independent?”) and the second capturing the intensity (e.g., “How strong or weak is your party affiliation?”). In the Nonbranching condition, both direction and intensity were captured in one question. The key takeaway from their abstract was, “We report eight experiments … demonstrating that fully labeled branching measures of party identification and policy attitudes are more reliable than partially labeled nonbranching measures of those attitudes. This difference seems to be attributable to the effects of both verbal labeling and branching.”
If all you read was the abstract, you’d think that full labeling was a better measurement practice than partial labeling. But when you review research, you can’t just read and accept the claims in the abstract. The figure below shows part of Table 1 from Krosnick and Berent (1993). Note that they list only three question formats. If their experimental designs had been full factorials, there would have been four. Missing from the design is the combination of partial labeling and branching. The first four studies also omitted the combination of full labeling with nonbranching, so any “significant” findings in those studies could be due to labeling or branching differences.
Image from Krosnick and Berent (1993) [pdf].
The fifth study at least included the Fully Labeled Nonbranching condition and produced the following results (numbers in cells are the percentage of respondents who gave the same answer on two different administrations of the same survey questions):
| Full | Partial | Diff | |
|---|---|---|---|
| Branching | 68.4% | NA | NA |
| Nonbranching | 57.8% | 58.9% | 1.1% |
| Diff | 10.6% | NA |
To analyze these results, Krosnick and Berent conducted two tests, one on the differences between Branching and Nonbranching holding Full Labeling constant and the second on the differences between Full and Partial Labeling holding Nonbranching constant. They concluded there was a significant effect of branching but no significant effect of labeling, bringing into question the claim they made in their abstract.
If you really want to understand the effects of labeling and branching on response consistency, the missing cell in the table above is a problem. Consider two possible hypothetical sets of results, one in which the missing cell matches the cell to its left and one in which it matches the cell below.
| Full | Partial | Mean | |
|---|---|---|---|
| Branching | 68.4% | 68.4% | 0.0% |
| Nonbranching | 57.8% | 58.9% | 1.1% |
| Difference | 10.6% | 9.5% |
| Full | Partial | Mean | |
|---|---|---|---|
| Branching | 68.4% | 58.9% | -9.5% |
| Nonbranching | 57.8% | 58.9% | 1.1% |
| Difference | 10.6% | 0.0% |
In the first hypothetical, the conclusion would be that branching is more reliable than nonbranching and labeling doesn’t matter. For the second hypothetical, the conclusion would be that there is an interaction suggesting that full labeling is better than partial, but only for branching questions and not for nonbranching. But without data for the missing cell, you just don’t know!
Summary and Discussion
When reading published research, it’s important to read critically. One aspect of critical reading is to identify whether the design of the reported experiment is confounded in a way that casts doubt on the researchers’ claims.
This is not a trivial issue, and as we’ve shown, influential research has been published that has affected social policy (Harlow’s infant monkeys), product claims (split keyboards), and survey design practices (labeling and branching). But upon close and critical inspection, the experimental designs were flawed by virtue of confounding; specifically, the researchers were drawing conclusions from incomplete factorial experimental designs.
In future articles, we’ll revisit this topic from time to time with analyses of other published experiments we’ve reviewed that, unfortunately, were confounded.