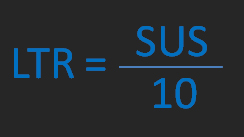 Introduced in 2003 by Fred Reichheld, the Net Promoter Score (NPS)® has become a popular metric of customer loyalty in industry.
Introduced in 2003 by Fred Reichheld, the Net Promoter Score (NPS)® has become a popular metric of customer loyalty in industry.
The NPS uses a single Likelihood to Recommend question (“How likely is it that you would recommend our company to a friend or colleague?”) with 11 scale steps from 0 (Not at all likely) to 10 (Extremely likely), as shown below.
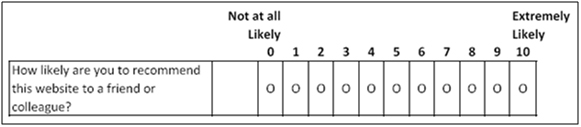
In NPS terminology, respondents who select a 9 or 10 are “Promoters,” those selecting 0 through 6 are “Detractors,” and all others are “Passives”. The NPS from a survey is the percentage of Promoters minus the percentage of Detractors, making the NPS a type of top-box-minus-bottom-box type of metric (actually, top 2 minus bottom 7 boxes) – thus, the “net” in Net Promoter.
For example, suppose you’ve collected 100 LTR ratings for a company for which 25 ratings fall between 0 and 6 (25% Detractors), 25 fall between 7 and 8 (25% Passives), and 50 fall between 9 and 10 (50% Promoters). The resulting NPS is the percentage of Promoters minus the percentage of Detractors, in this case, 25%. The developers of the NPS hold that this metric is easy for managers to understand and to use to track improvements over time, and that improvements in NPS have a strong relationship to company growth[pdf]. The metric becomes especially valuable when compared to industry benchmarks.
Since its introduction, the NPS has generated controversy. For example, Keiningham et al. (2007, 2008) challenged the claim of a strong relationship between NPS and company growth. In general, top-box and top-box-minus-bottom-box metrics lose information during the process of collapsing measurements from a multipoint scale to percentages of a smaller number of categories, and thus lose sensitivity (although increasing sample sizes can make up for lack of sensitivity in a metric).
Despite these criticisms, it is unlikely that the popularity of the NPS will diminish at any time in the near future due to its simplicity and intuitiveness.
* Our friends at Satmetrix want us to remind you that Net Promoter, NPS, and Net Promoter Score are trademarks of Satmetrix Systems, Inc., Bain & Company, and Fred Reichheld
The System Usability Scale (SUS)
Despite being a self-described “quick and dirty” usability scale, the System Usability Scale (SUS), developed in the mid 1980s by John Brooke, has become a popular questionnaire for end-of-test subjective assessments of usability.
The SUS accounted for 43% of post-test questionnaire usage in a recent study of a collection of unpublished usability studies. Research conducted on the SUS has shown that although it is fairly quick, it is probably not all that dirty.
The Initial Regression Equation from January 2010
Two years ago we published a regression equation for predicting someone’s likelihood to recommend (LTR) a product given their System Usability Scale (SUS) score. That equation was:
In other words, to convert a SUS score (which ranges from 0 to 100), into an LTR rating (which ranges from 0 to 10), you’d take 9% of the SUS score then add about .5. Analysis of the regression indicated that the SUS scores explained about 36% of the variation in LTR ratings (which corresponds to a statistically significant correlation of about .6 between SUS and LTR).
Revisiting the Regression Equation
After publishing the initial equation (for which n = 146), we continued collecting LTR and SUS data, increasing the number of individual pairs of scores to just over 2200 (distributed over 81 companies with sample sizes ranging from 4 to 113). With this new data added, the resulting regression equation is:
LTR = 1.33 + 0.08(SUS)
Although the parameters of the equation are somewhat different, this equation isn’t dramatically different from the initial one. The intercept is somewhat greater (1.33 instead of 0.52) and the slope is a little less steep (8% instead of 9%). The percentage of variation in LTR explained by SUS is slightly higher (about 39%, corresponding to a statistically significant correlation between LTR and SUS of .623).
When you change the data from which you derive a regression equation, you expect some change in the parameters, so this shouldn’t be shocking news – especially with this sample size roughly 15 times the size of the initial sample.
Simplifying the Regression Equation
The good news is that the regression equation you get from applying standard least squares methods provides a constant and a slope that guarantees minimal prediction error for the data used to provide the estimates. The bad news is that the resulting equation isn’t likely to be easy to remember.
One of the things Jeff and I noticed with both regression equations was that the slope was almost equal to 0.1 (10%), so we wondered what would happen to the quality of the regression equation if we dropped the intercept (mathematically, forcing its value equal to 0). If it turned out that this changed the slope to 10%, then it would result in a very easy to remember relationship between LTR and SUS – if you know the SUS score, just divide it by 10 to get an estimate of the user’s likelihood to recommend.
LTR = 0.1(SUS)
LTR = SUS/10
Whenever you deviate from the parameters indicated by least squares regression, you expect the quality of the regression formula as measured by its coefficient of determination (the percentage of variance explained) to decline. The question was how much quality we would lose as a consequence of this simplification.
It turned out that the percentage of variation in LTR explained by SUS for the simplified equation was about 37% (corresponding to a statistically significant correlation of about .606) – a drop of only 2%. If you don’t remember the updated equation, you will get almost as good a prediction with the easier-to-remember simplified equation.
Using the Regression Equations
If you have existing SUS scores from usability evaluations, you can use either of these regression equations to estimate LTR, and from those LTR estimates, compute the corresponding estimated NPS. A shortcut calculator is provided below which will also convert the LTR Score to a Net Promoter Score.
SUS to Net Promoter Score Converter
Enter a mean to get an estimated Net Promoter Score or enter an NPS to get the estimated mean.
This can be helpful if your company is using NPS from other voice-of-the-customer sources as a consistency check. If you’re serious about using LTR in the future, it is a small effort to collect ratings of the LTR item in addition to the SUS rather than estimating it.
 About Jim Lewis PhD : Jim has worked as a human factors engineer and usability practitioner at IBM since 1981. He has published influential research on the measurement of usability satisfaction, use of confidence intervals, and sample size estimation for usability studies.
About Jim Lewis PhD : Jim has worked as a human factors engineer and usability practitioner at IBM since 1981. He has published influential research on the measurement of usability satisfaction, use of confidence intervals, and sample size estimation for usability studies.
He is a BCPE Certified Human Factors Professional, an IBM Master Inventor, and a member of UPA, HFES, APS and APA. He is the author of Practical Speech User Interface Design (Taylor & Francis 2011) and is co-author of the forthcoming book Quantifying the User Experience (Morgan Kaufmann 2012).


