
You don’t need to be a mathematician to quantify the problems and improvements in user interfaces.
Often the most compelling metrics are simple to compute and require no more than arithmetic and basic algebra.
While most of us were exposed to these concepts in 8th and 9th grade, they are easy to forget and probably didn’t seem applicable when not learned in context.
Here are eight fundamental concepts to help with quantifying the user experience.
- A percentage and proportion are used interchangeably: A proportion is as it sounds–part of a total. If eight out of 10 users can locate an item in your navigation then the proportion successful is 8/10 = .8. This is usually expressed as a percentage which involves moving the decimal to the right two positions (multiplying the proportion by 100). So .8 becomes 80% successful or just an 80% completion rate. You can also subtract the successful proportion from 1 to get the failure rate : 1-.8 = .2 and express that as a percentage: 20% failure rate.
- Percentages can be used on any sample size: Percent literally means “per 100.” There is a perception that you have to have a large sample size (above 30 or 100) to use “percent.” You can compute a proportion or percent on any sample size. Of course very small samples mean the percentage, while a good guess of the total population’s percentage, is almost surely wrong. Confidence intervals around any percentage can be used to provide the most plausible range of the unknown population proportion.
- To show an increase or decrease in a value use the following services: Take the base amount and subtract the alternate amount. Divide this value by the base amount. For example, if the average time it took to register on a website went from 100 seconds on the old design(base amount) down to 70 seconds on the new design (alternate amount), it is a reduction in time of 30%.
(Base Amount – Alternate Amount)/ Base Amount
( 100 – 70 ) / 100 = .3 or 30% expressed as a percentageYou can also make a statement about how much longer the old time was compared to the new time. We take the same values but switch our bases.
( 70 – 100 ) / 70 = -.429 or -43%.
Because negative percentages can be difficult to interpret, I take the -43% and say the old time took 43% longer than the new design. Both are different ways of expressing the same outcome, but the first is more common.
- Percentage increases are different than percentage point increases: Going from 30% to 33% is a 10% increase but a 3 percentage point increase. What you choose to call it largely depends on your motivation and the audience motivation. Most people will associate a 3 point increase with a 3% increase. A 3 point increase doesn’t sounds nearly as impressive or ominous as a 10% increase. If it’s regarding completion rates or conversation rates you’ll probably use the 10% increase. If it’s about raising someone else’s taxes it will be a 3 point increase.
- Order of operations: Usability’s most famous equation is 1 –(1-p) n . It tells you the percent of problems with a probability of occurrence (p) that you’d see if you tested a given number of (n) users. It’s based on the binomial probability formula and is at the heart of the magic number 5 in sample size planning. The p (sometimes lambda) is how common a usability problem is (expressed as a proportion). For example, if a problem affects 1 out of 3 users, p is .333. The value “n” is the sample size. To solve the equation you work from the innermost parenthesis, then exponentiation, then subtraction.For example, if you test five users, what are the chances you’ll see a problem that impacts 31% of all users?
1 –(1-.31) 5
1 –(.69) 5
1 – .1564
.843597
Expressed as a percentage, there’s an 84.4% chance you’d see the problem after testing with five users. If a problem affects only 1 out of 10 users, you’d have a 41% chance of seeing a problem with that frequency after testing with five users.
- There are many “averages”: The arithmetic mean is the most common measure of the middle of data but the median and mode are other famous measures of “central tendency.” The geometric and harmonic means are also frequently used in the behavioral sciences but are less famous averages.The median is a better measure of the center of a set of data when there are a few extreme values—such as home prices a city or salaries at a company. The mean is heavily influenced by just a single large value, whereas the median is much more stable against extremes. The graph below shows the completed task times for 50 users trying to locate the nearest Budget rental car office. The arithmetic mean is 133 seconds and the median time is 120 seconds. The high mean is due to the influence of the two times at around 350 seconds.
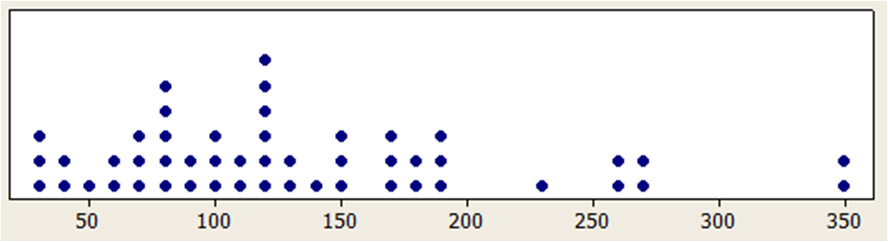
Figure 1: Task times (in seconds) for 50 users locating the nearest Budget rental car location. The median time of 120 seconds isn’t affected as much as the mean (133 seconds) by the few users that took long.
-
- Logarithm : It’s just a reverse exponent. It’s used to lessen the effect of extreme values in things like salaries, home prices and time-on-task data. It is usually the case that the slowest users to complete a task can take 5 to 10 times longer than the fastest (as seen in the example above). These slower users pull the arithmetic mean well above the center point.Logarithms are confusing but there’s some evidence we think with them more naturally. One problem is the word logarithm has little meaning today. What’s the log and where’s the rhythm? If you change the word logarithm to magnitude it might make more sense. The famous Richter Scale for measuring the magnitude of earthquakes is logarithmic.We found that the geometric mean is a better measure of the middle than the median when sample sizes are less than about 25. The geometric mean is found by taking the average of the logarithms, then transforming back.
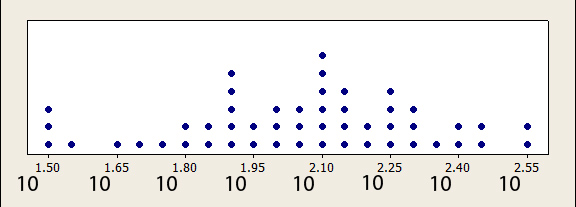
Figure 2: Log transformed task times from Figure 1. The log transformation pulls in the longer times and makes the arithmetic mean a better measure of the center. A raw time of 350 seconds becomes 2.54, which is 10 raised to the power of 2.54.
Most of us are comfortable with exponents: 102 is 100 and 103 is 1000. A logarithm is the reverse of an exponent. What exponent on 10 will get you 1000? This answer is 3. That is, the logarithm of 1000 is 3. If you get stuck, try thinking, what magnitude gets you 1000? Hopefully you’ll remember that it’s 10 to the power of 3. Most calculators have a Log button and in Excel you can use the formula =LOG10().
-
-
- The Standard Deviation and the Variance are used interchangeably but are slightly different: The standard deviation is the most common measure of variability. It can be thought of as the average difference each value is from the mean. With a measure of the center and a measure of variability you can describe almost all sets of data. The variance is the standard deviation squared. So like the percentage and proportion, if you have one you can get the other. While we almost always communicate variability using the more intuitive standard deviation, the variance is used more behind the scenes in formulas. You can’t add and subtract square roots, which of course you remember from 9th grade algebra!
-


