Minimize Lurking Variables
Getting Warmed Up
Without task randomization, so-called lurking variables can taint your data–usually not enough that it’s devastating but often it’s noticeable. One lurking variable when analyzing task times is the user’s tendency to perform better on the later tasks and worse on the earlier tasks. It’s human nature: someone hands you a piece of paper and says: “Ok, complete the task. ” Sometimes it takes the user a few tasks to get warmed up and acquainted with the process (not to mention getting used to being recorded).
Immediate Prior Exposure
Also as the user completes more tasks they are being exposed to more parts of the interface, reminding them of the structure and where to find functions. In the later tasks, the user might be asked to complete a task and will recall seeing the function while completing a a prior task. As a consequence they perform the task more quickly than they otherwise would have. By randomizing your tasks you distribute the efficiency effect over all tasks instead of the same later tasks.
Detecting Lurking Variables
One way to detect if there is an effect on tasks times as the test session progresses is to analyze the the difference in time between the user’s time on task from the task mean. This is a comparison of deviations by task. To calculate the deviation, first calculate the mean for each task. Next take each user’s time and subtract it from the mean then squre it to eliminate negative times (when a user completes the task faster than the mean time, their deviation is negative, squaring it preserves the spread from the mean).
Deviation = (user time – mean time)^2
Plot the deviation for each task by the order the task was administered for each user. You can use a Run Chart in Mini-tab. Look visaully for trends. Most Run Chart’s need a minium of 20 data points for reliable readings
Plotting Deviations
The following sample data only contains 13 data points between eleven users. I don’t throw away the data because there are less than twenty data points, instead I look for stronger p-values and know that any conclusions should be made with caution.
Figure 1: Run Charts of Deviations by Task Order for All Users
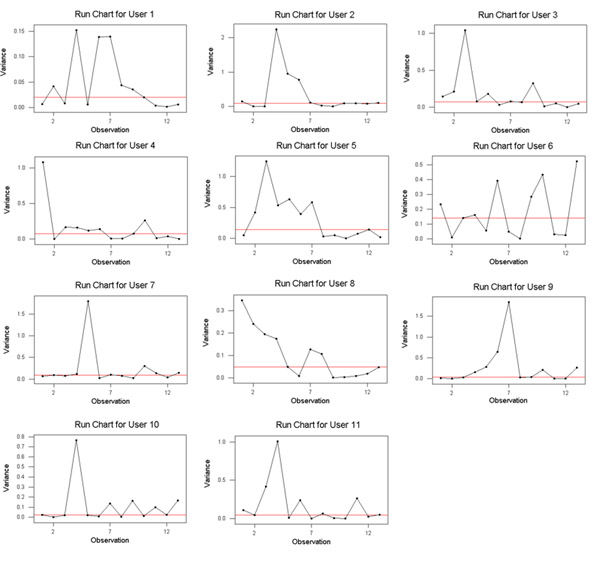
Notice User 8’s Run Chart. Visually it looks like there is a reduction in deviation as the tasks progress. Whereas user User 6 doesn’t appear to have any trends. User 8 has a p-value of .00106 for trends and User 6 has a p-value of .40658 confirming our initial visual impression.
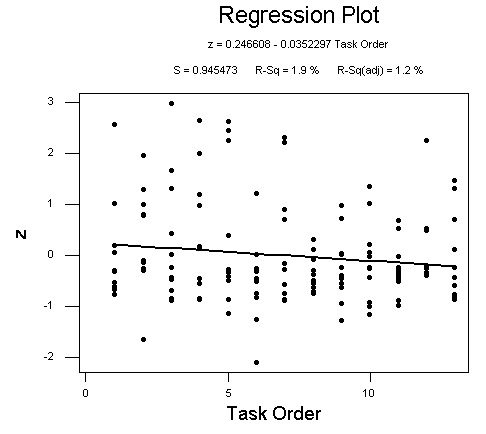
Comparing Z-Scores for all tasks
If we wanted to compare the variation for all tasks we would need a way to control for the difference in tasks times. For example, one task might have a mean time of 200 seconds and a standard deviation of 30 seconds whereas another task may have a mean time of 30 seconds and standard deviation of 8 seconds. To control for the differences obtain a z-score for all tasks using the following formula:
z-score = (task time – mean time)/ standard deviation
Now plot the z-scores using the same run chart.
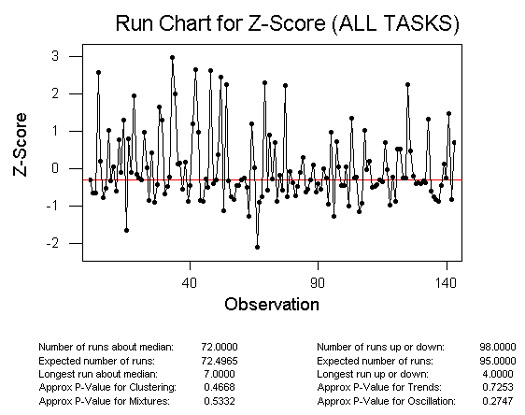
Based on my sample data, no significant p-values appear in the run chart for trends, oscillation, mixtures or clustering. Taking the same data I plottted the z-scores with a regression line. As you can see, there is a slight decrease in z-score variation as the tasks progress. Notice that the r-square is only 1.9%. That means that task order accounts for less than two percent of the variation in z-scores.