 What sample size do we need?
What sample size do we need?
It’s consistently among the most common questions I get from researchers.
It can be a confusing process, but that’s why we cover sample-size planning at the Denver UX Boot Camp.
Determining the right sample size for a project is a science–an imprecise science.
It’s like appraising a house: you make assumptions, some more accurate than others, but rarely does an appraisal match the final sale price of the home exactly. But a good appraisal, like a good sample size estimate, gets you close.
Determining sample size involves identifying the type of metrics you’ll collect and how you’ll collect them. Typically, you take one of three approaches to find the right sample size:
- uncovering problems or insights
- estimating a parameter
- making a comparison
We’ll look at eight research studies and discuss how to determine the sample size for each.
Uncovering Problems or Insights
Uncovering problems or looking for insights entails two main factors: how common they are and the probability you’ll detect them with a sample of users.
- A formative usability test: This is the classic find-and-fix usability study. To determine the sample size, estimate how common the usability problems are and then determine a sample size that has a good chance of uncovering those problems. For example, to have a good chance of seeing more obvious issues (those that affect at least 30% of users), test 5 participants. If a usability problem exists and impacts only 10% of the customer base, then test 21 participants.
- Finding customer requirements: The number of customers to observe or interview to discover insights is a function of how common the issues are. For more common requirements or behaviors, you’ll see redundancy after a few customers. For less common behaviors or requirements, you have to observe more participants. For example, if 20% of customers struggle exporting data from a point-of-sale machine into QuickBooks, then observing 9 customers affords an 85% chance of seeing that behavior.
The values in Table 1 below show you the sample size needed for an 85% chance of seeing problems or observing a behavior at least once, based on your estimation of how common they are.
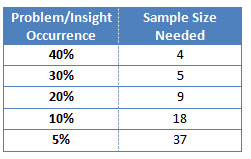
Table 1: Sample size needed to have an 85% chance of observing a problem or behavior at least once.
Estimating a Parameter
To estimate a parameter, work backwards from a confidence interval to compute the sample size. The result is a statement like this: “We are 95% confident that between 60% and 70% of customers would agree to repurchase the service plan.” To compute the sample size needed to make that statement, you need the following:
- Standard deviation (for continuous metrics) or an estimate of a percentage for binary data. Rarely do researchers know the standard deviation for continuous metrics so we often use the binary percentage.
- Confidence level: typically 90% or 95%, but flexible, based on the need for precision.
Table 2 (below) shows recommended sample sizes for the next four scenarios.
- A benchmark usability test (emphasis on metrics): While benchmark usability studies also involve problem identification, they emphasize assessing the usability of an experience. A good usability-benchmark study includes metrics to measure effectiveness (completion rates), efficiency (time), and customer satisfaction (post-task and post-test questionnaires). We use the metric with the highest variability to estimate sample size: the binary completion rate. For example, a sample size of 93 provides a margin of error of +/- 10% for a 95% level of confidence. See the row that starts at 10% in Table 2 below.
- A standalone survey: In surveys not involving comparison, we use a sample of customers to estimate the sentiments of the entire customer population. Use a confidence interval around sample means (average satisfaction rating or agree/disagree statements, for example). Surveys usually combine binary and continuous data; and since binary data has the wider confidence intervals, we use them to compute our sample size. At a sample size of 53, for example, the expected margin of error is ~13% for 95% confidence, which means that if 70% of respondents agree to a statement, then we can be 95% confident that between 57% and 83% of all customers will agree to the statement.
- A navigation study: To test the effectiveness of a taxonomy (categories and labels), use a tree test. A tree test provides measures of findability (a binary metric), time, and difficulty. A tree test is basically a special kind of usability test and we’ll therefore use the same binary approach to compute the needed sample size. To estimate the findability rate with a 7% margin of error and 90% confidence, we have 136 participants complete the tree-test study (see the row in Table 2 that starts with 7%).
- Card-sorting study: Card sorting enables us to understand how our users group products, items, or information in a website or application. Card sorting uses various clustering algorithms based, typically, on a similarity matrix—a grid of proportions indicating how often participants group an item into a category. For example, if 20 out of 30 people put “prom dress” in the category of “teens,” the proportion in the similarity matrix is 0.67.We can now estimate the sample size we need to understand how much that proportion would fluctuate if we were to sample more participants. For that proportion to fluctuate by no more than 15 percentage points, and for a 90% confidence level, we specify a sample size of 28 (see the row in Table 2 that starts with 15%).
Some evidence suggests that while proportions fluctuate, clusters formed by participants fluctuate far less and thus require a smaller (often less than 20) sample size. We have replicated some of these findings, but the results may be a function of the homogeneity of the categories and items; more research is needed.
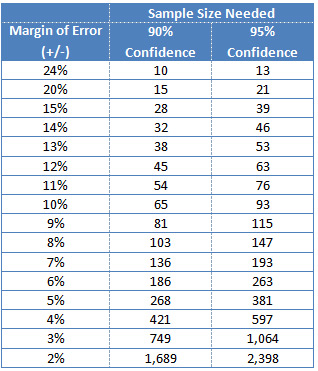
Table 2: Sample size needed for specific margins of error for 90% and 95% confidence levels.
Making Comparisons
When you’re comparing, three more factors come into play:
- The size of the difference you want to detect: smaller differences require larger sample sizes.
- Within or Between Subjects: Using the same participants on both products being tested is called a within-subjects study. Using different participants on each product is a between-subjects study. Because differences between people often outweigh differences in interfaces, a within-subjects approach, when you can use it, enables you to detect statistical differences with smaller sample sizes. It’s a major factor when determining sample sizes.
- The ability to detect a difference (Power): This is like the confidence level for detecting a difference if one exists. This is usually set to 80%, but you can vary it based on the type of study.
- Design comparison study: If you want to know which design participants think is better or perform better on, your sample size is a function of how small a difference you hope to detect (if one exists). You’ll most likely use a combination of binary metrics and rating scales, so use the binary metrics to set the sample size. The most conservative approach is to assume that the responses percentage will hover around 50% (which is the highest variability).For example, if you want to detect a 10% difference between designs, use a sample size of 614 (307 assigned to each design) for a between-subjects approach. At a sample size of 426 (213 in each group), we can detect a 12% difference for a between-subjects design. So if 50% agree to a statement on one website and 62% on a competitive site, the difference would be statistically significant. A within subjects study would require only 93 participants (less than 25% of the between-subjects sample size).
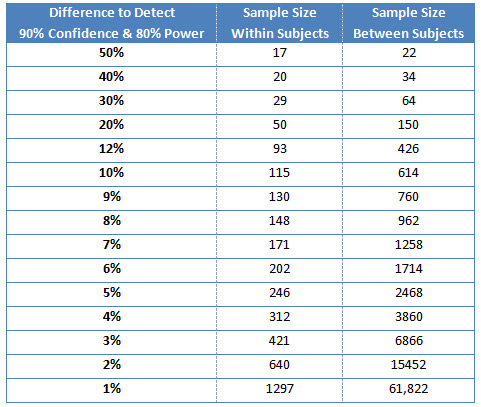
Table 3: The approximate difference we can detect in metrics such as the completion rate or any other binary measure (at a 50% completion rate or agreement rate), using 90% confidence and 80% Power.
These estimates are the most conservative but are recommended when planning a study without prior data. For continuous measures like perceived difficulty, branding, and overall perceptions, we can detect smaller differences at the same sample size (but you’ll need some estimate of the standard deviations).
8. A/B test: An A/B test on a website typically involves detecting relative small differences based on a conversion rate (also a binary metric). A/B tests are run as between-subjects studies; participants going about their usual business are randomly assigned one of two alternatives. Conversion rates in A/B tests often hover below 5%—usually below 1%, in fact. This is substantially reducing the variability in the results, and so requires smaller sample sizes.
For example, to detect a 1-percentage-point difference in conversion rates (e.g., 5% to 6%), test 12,856 users. This seems like a huge sample, but it’s less than one-fourth the sample size you’d need if the conversion rate hovered around 50% (last row in table 3).
Table 4 shows the sample size needed to detect differences as small as 0.1% (over half a million in each group) or as large as 50% (just 11 in each group).
| Sample Size | ||||
| Difference | Each Group | Total | A | B |
| 0.1% | 592,905 | 1,185,810 | 5% | 5.1% |
| 0.5% | 24604 | 49,208 | 5% | 5.5% |
| 1.0% | 6428 | 12,856 | 5% | 6.0% |
| 5.0% | 344 | 688 | 5% | 10.0% |
| 10.0% | 112 | 224 | 5% | 15.0% |
| 20.0% | 40 | 80 | 5% | 25.0% |
| 30.0% | 23 | 46 | 5% | 35.0% |
| 40.0% | 15 | 30 | 5% | 45.0% |
| 50.0% | 11 | 22 | 5% | 55.0% |
Table 4: Sample size needed to detect differences from .1% to 50%, assuming 90% confidence and 80% power and conversion rates hovering around 5%.
In Summary
In Chapters 6 and 7 of Quantifying the User Experience, we describe the calculations used to compute the sample sizes in these tables. It takes time to determine the right sample size, so, before you start, be sure you know which type of computation your research design falls into:
- uncovering problems or insights
- estimating a parameter
- making a comparison
To generate more precise sample sizes, you’ll need a little practice—and the stats calculator I put together helps a lot too!


