 Researchers rely heavily on sampling.
Researchers rely heavily on sampling.
It’s rarely possible, or even makes sense, to measure every single person of a population (all customers, all prospects, all homeowners, etc.).
But when you use a sample, the average value you observe (e.g. a completion rate, average satisfaction) differs from the actual population average.
Consequently, the differences between designs or attitudes measured in a questionnaire may be the result of random noise rather than an actual difference—what’s referred to as sampling error.
Understanding and appreciating the consequences of sampling error and statistical significance is one thing. Conveying this concept to a reader is another challenge—especially if a reader is less quantitatively inclined.
Picking the “right” visualization is a balance between knowing your audience, working with conventions in your field, and not overwhelming your reader. Here are six ways to indicate sampling error and statistical significance to the consumers of your research.
1. Confidence Interval Error Bars
Confidence intervals are one type of error bar that can be placed on graphs to show sampling error. Confidence intervals visually show the reader the most plausible range of the unknown population average. They are usually 90% or 95% by convention. What’s nice about confidence intervals is that they act as a shorthand statistical test, even for people who don’t understand p-values. They tell you if two values are statistically different along with the upper and lower bounds of a value.
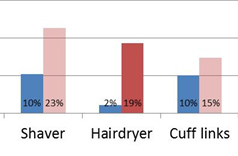
That is, if there’s no overlap in confidence intervals, the differences are statistically significant at the level of confidence (in most cases). For example, Figure 1 shows the findability rates on two websites for different products along with 90% confidence intervals depicted as the black “whisker” error bars.

Figure 1: Findability rates for two websites. Black error bars are 90% confidence intervals.
Almost 60% of 75 participants found the sewing machine on website B compared to only 4% of a different group of 75 participants on website A. The lower boundary of website B’s findability rate (49%) is well above the upper boundary of website A’s findability rate (12%). This difference is statistically significant at p < .10.
You can also see that the findability rate for website A is unlikely to ever exceed 15% (the upper boundary is at 12%). This visually tells you that with a sample size of 75, it’s highly unlikely (less than a 5% chance) that the findability rate would ever exceed 15%. Of course, a 15% findability rate is abysmally low (meaning roughly only 1 in 7 people will ever find the sewing machine).
This is my preferred method for displaying statistical significance, but even experienced researchers with strong statistics backgrounds have trouble interpreting confidence intervals and they aren’t always the best option, as we see below.
2. Standard Error Error Bars
Another type of error bar uses the standard error. These standard error error bars tend to be the default visualization for academia. Don’t be confused by the name—standard error error bars aren’t necessarily the “standard.” The name is due to the fact that they display the standard error (which is an estimate of the standard deviation of the population mean). For example, Figure 2 shows the perceived ease for a task on four retail websites using the Single Ease Question (SEQ) and the standard error for each.
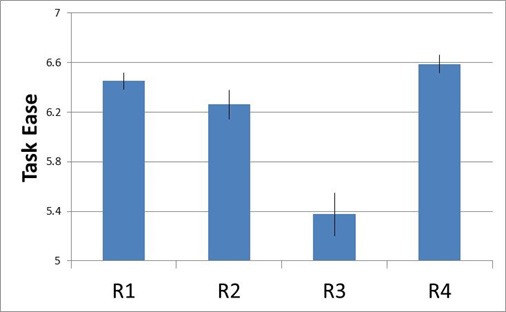
Figure 2: Perceived ease (using the SEQ) with standard error error bars for four retail websites.
The standard error is often used in multiple statistical calculations (e.g. for computing confidence intervals and statistical significance) so an advantage of showing just the standard error is that other researchers can more easily create derived computations.
The main disadvantage I see is that people still interpret it as a confidence interval, but the non-overlap no longer corresponds to the typical thresholds of statistical significance. Showing one standard error is actually equivalent to showing a 68% confidence interval. The 90% confidence intervals for the same data are shown in Figure 3. You can see the overlap in R1 and R2 (meaning they are NOT statistically different); whereas the non-statistical difference is less easy to spot with standard error error bars (Figure 2).
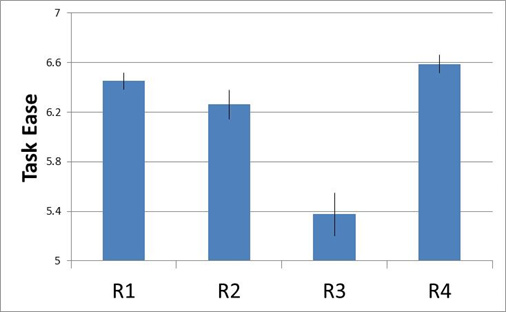
Figure 3: Perceived ease and 90% confidence intervals for four retail websites.
3. Shaded Graphs
Error bars of any kinds can add a lot of “ink” to a graph, which can freak out some readers. A visualization that avoids error bars is to differ the shading on the bars of a graph that are statistically significant. The dark red bars in Figure 4 show which comparisons are statistically significant. This shading can be done in color or in black-and-white to be printer friendly.
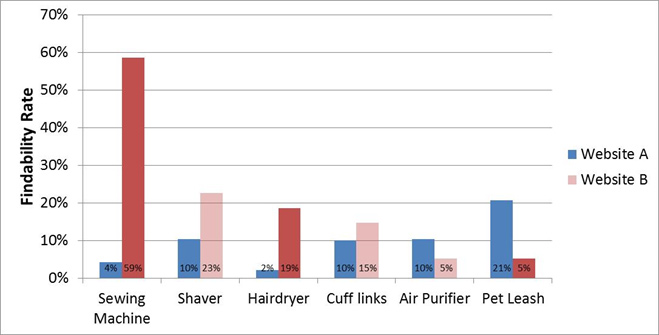
Figure 4: Findability rates for two websites; the dark red bars indicate differences that are statistically significant.
4. Asterisks
An asterisk (*) or other symbol can indicate statistical significance for a modest number of comparisons (shown in Figure 5). We’ve also seen (and occasionally use) multiple symbols to indicate statistical significance at two thresholds (often p
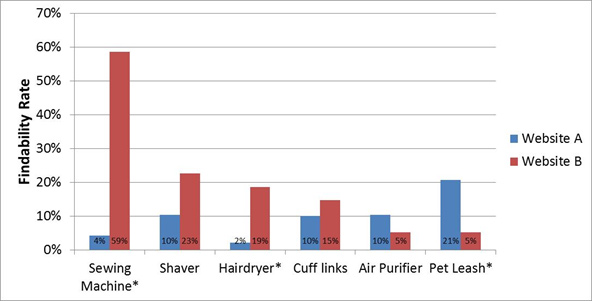
Figure 5: Findability rates for two websites; asterisks indicate statistically significant differences.
5. Notes
It’s often the case that so many comparisons are statistically significant that any visual indication would be overwhelming (or undesired). In those cases, a note depicting significance is ideal. These notes can be in the footer of a table, the caption of an image (as shown in Figure 6), or in the notes section of slides.
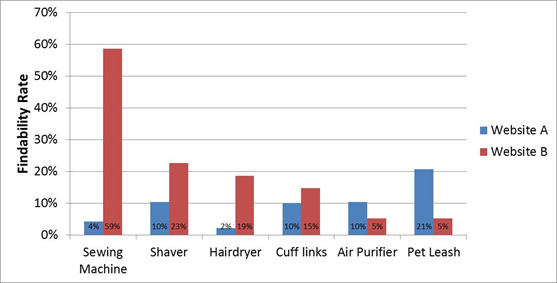
Figure 6: Findability rates for two websites. Sewing Machine, Hairdryer, and Pet Leash findability rates are statistically different.
6. Connecting Lines and Hybrids
When differences aren’t contiguous an alternative approach is to include connecting lines as shown in Figure 7 below. It shows 8 conditions in a UX research study using three measures (satisfaction, confidence, likelihood to purchase). Three differences were statistically different as indicated by the connecting lines. The graph also includes 95% confidence intervals and notes in the caption.
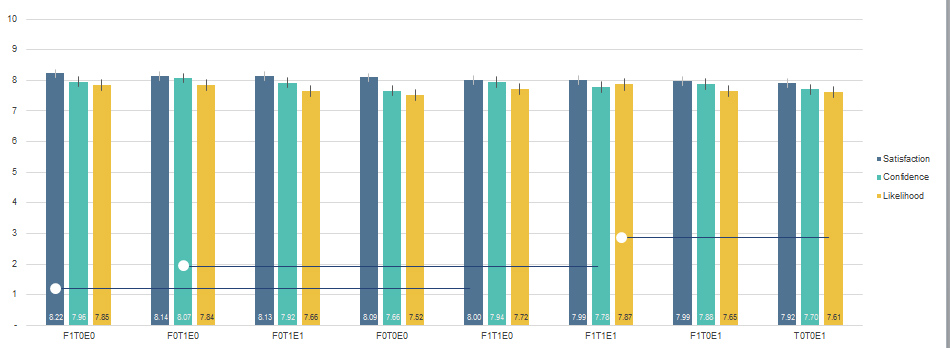
Figure 7: Mean satisfaction, confidence and likelihood to purchase across 8 conditions. Error bars are 95% confidence intervals. Connecting lines show statistical differences for conditions: satisfaction F1T0E0 vs. F1T1E0; confidence F0T1E0 vs F1T1E1; and likelihood to purchase F1T1E1 vs. T0T0E1.


