How Do You Calculate a Z-Score/ Sigma Level?

The benefit of using a z-score in usability metrics was explained in “What’s a Z-Score and why use it in Usability Testing?” this article discusses different ways of calculating a z-score.

The short answer is: It depends on your data and what you’re looking for. If you’ve encountered the z-score in a statistics book you usually get some formula like:

The above formula is for obtaining a z-score for an entire population. Usability testing obviously samples a very small subset of the population and thus the following formula is used:

Where x-bar and s are used as estimators for the population’s true mean and standard deviation. Both formulas essentially calculate the same thing:

Calculating a Z-Score Example

For example, lets say you took the GRE a few weeks ago and got scores of 630 Verbal and 700 Quantitative. How good are these scores? Which is better, the Verbal or Quantitative score? Using a z-score can tell you how far you are from the mean and thus how well you performed. If you know the mean and standard deviations for a set of GRE test takers you can compare your scores.

 

ETS publishes the means and standard deviations of a set of test takers on the GRE website.

	Verbal	Quantitative
Mean	469	591
StDev	119	148

By plugging in your scores you get the following:

Verbal z = (630 – 469) ÷ 119 = 1.35σ

Quantitative z = (700 – 591) ÷ 148 = .736σ

To convert these sigma values into a percentage you can look them up in a standard z-table, use the Excel formula =NORMSDIST(1.35) or use the Z-Score to Percentile Calculator (choose 1-sided) and get the percentages : 91% Verbal and 77% Quantitative. You can see where your score falls within the sample of other test takers and also see that the verbal score was better than the quantitative score. Assuming the sample data was normally distributed, here’s how the scores would look graphically:

Figure 1: Verbal Score

Figure 2: Quantitative Score

 

Z-Scores and Process Sigma

An interactive Graph of the Standard Normal Curve similar to Figures 1 & 2 is available for you to visualize how the z-scores and the area under the normal curve correspond. The graphs also allow you to see the difference between one and two-sided (also called two-tailed) areas. In Six Sigma the process sigma metric is derived using the same method as a z-score. However, in Six Sigma you are measuring the distance a sample mean is above a specification limit–there can be an upper and lower spec limit that a sample must fall between as well. As in the z-score, you still use the same normal-deviates from the z-table to approximate the area under the curve. The process sigma metric is essentially a Z equivalent.

 

When testing software with users, task times are usually a good metric that will reveal the individual differences in performance. For task times there typically is only an upper spec limit. That is, it usually doesn’t matter how fast a user completes a task, but it does matter if a user takes too long. For example, say you and your product team determined that a task should be completed in 120 seconds. 120 seconds becomes your Upper Spec Limit (USL). You sampled 10 users and got these task times:

 

Sample

100 99 101 125 100 123 96 90 98 116

USL: 120 Mean: 104 StDev: 12

To calculate the process sigma you subtract the mean (104) of the sample from the target (120) and divide by the sample standard deviation (12). For Sample 1 the process sigma is -1.32σ. The visual representation of the data can be seen below:

In the case of task times, a negative process sigma is ideal–as you want more people completing the task below the task time, not above it. You can simply drop the negative when communicating the results in the event it causes confusion. If you were to make radical improvements to the UI and then sampled another set of ten users, here are more results:

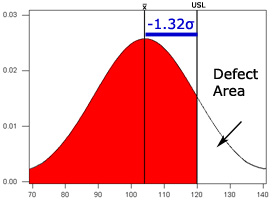
Sample 2

60 75 99 88 65 72 75 72 87 65

USL: 120 Mean: 75.8 StDev: 12.14

In the redesign, the average of the new sample is well below the spec limit and the process sigma is now very high. The corresponding defect area is now only .01% and the quality area is 99.98%

Of course having users perform that much below the spec limit is not very common due to the inherent variability in user performance.

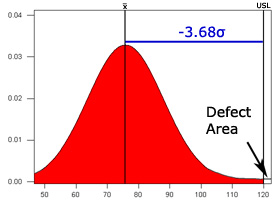
If you need more help with z-scores, see the Crash course in Z-scores, a tutorial with plenty of pictures, examples and review questions for you to grasp this concept.