 You can slice and dice data in a lot of ways using a variety of statistical tests.
You can slice and dice data in a lot of ways using a variety of statistical tests.
The type of study, data type, and your research question will dictate the right statistical test you need to perform.
With the five tests I cover here, you can test most of your hypotheses in the customer experience. I’ll discuss all five tests in detail at the Denver UX Boot Camp.
1. Confidence Interval for Binary Data
You usually sample only a small fraction of a customer base when you collect metrics. You’ll deal with sampling error when you don’t sample the entire customer population. To understand how accurate a sample is (and how much sampling error you have) you use confidence intervals. The Adjusted Wald confidence interval works on binary categorical data (pass/fail, convert/didn’t convert) on any sample size. It works like this:
- Convert the categorical data into 1s and 0s, where 1 is a pass and 0 is a fail.
- Compute the confidence interval using the online calculator. For example, if 15 out of 16 employees in a company agreed to the statement “I love learning statistics,” then 94% in the sample agree.
- To estimate what percent of all employees will agree, use the Adjusted Wald confidence interval calculator (shown below).
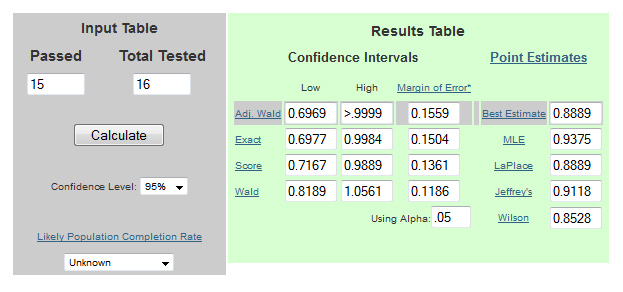
Assuming the sample was reasonably random when selected from the company, you can be 95% confident that between 70% to 99% of all employees would also love learning statistics. More details on this method are in Chapter 3 of Quantifying the User Experience.
2. Confidence Interval for Continuous Data
You can treat the ubiquitous data from rating scales and questionnaires as continuous data. The confidence interval is based on the t-distribution, which works on any sample size and is reasonably robust against violations of normality. You can use raw data or summarized data to compute the confidence interval. If you don’t have access to the raw data, all you need is the mean, standard deviation, and sample size.
For example, we had 30 participants attempt to create an account in a web application and had them rate the task ease on the 7-point SEQ. The average response was a 6.33 and the standard deviation was .91. I plugged these values in the online calculator shown below.
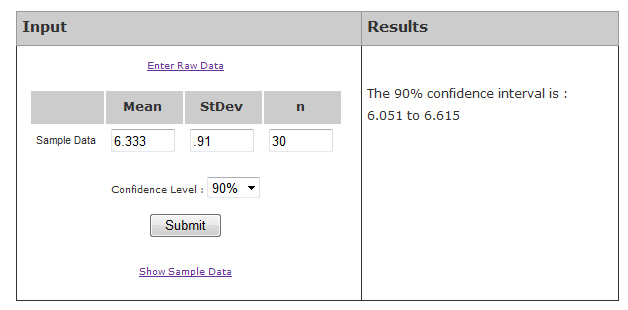
The 90% confidence interval is about 6.1 to 6.6. If thousands more participants attempt to create an account on this web app, the average ease rating would unlikely be lower than 6.1 or higher than 6.6. Given the average difficulty across the SEQ is 5.1, a low of 6.1 indicates this is an easier than average task, which is good as you don’t want it to be too difficult to create an account!
3. 2-Sample t-Test
When you want to compare two sets of continuous data (rating scales, survey items, task-times) use the 2-sample t-test. It works well with any sample size and is robust to violations of normality and unequal variances. It’s the workhorse of statistical tests. Like most statistical tests, the output is a p-value.
You can compare the account creation score from the previous example to another web application’s account creation process. In this case, eight participants found the process of creating an account more difficult (it also took three times as long!). Their average score on the SEQ was 2.75 with a standard deviation of 1.67. That’s almost a 4 point difference compared to the 6.33, but there are only 8 scores. What are the chances of seeing a difference that large if there really was no difference?
Again all you need is the mean, standard deviation, and sample size for both sets of data. I’ve plugged those values in the 2-sample t-test calculator shown below.
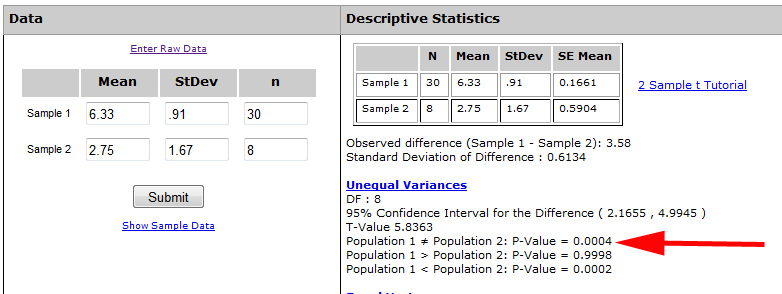
The p-value is less than .001 (see the red arrow in the figure). In other words, even though the sample size is small in one group, the difference is so large, that you’d expect to only see a greater than 4 point difference if there really was no difference about four times in ten thousand (p = .0004). With such a low chance the difference is statistically significant.
Note: This calculator assumes different people are in each sample. If the same people are used in both samples, you need to compute a paired t-test.
4. 2-Proportion Test (A/B)
For comparing two proportions, such as task-completion rates, agreement rates, or conversion rates (such as A/B tests), use the 2-proportion test. The online calculator works for all sample sizes. For example, if you asked another sample of employees if they enjoy doing annual performance reviews and 7 out of 12 respondents agreed, you can compare this proportion (.58) against the proportion that like learning statistics from the first example (15 out of 16 = .94). I entered the data in the online calculator shown below.
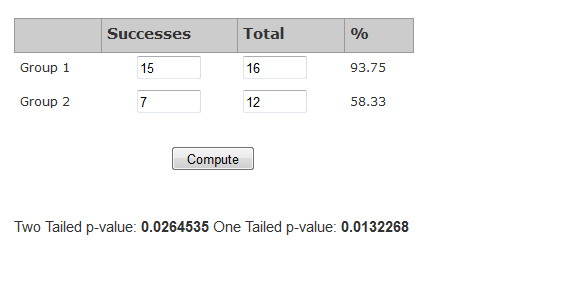
You get a two-tailed p-value of .0264 (more on the difference between one and two tails). The probability of seeing that large of a difference if there really was no difference in agreement rate is 2.64%. Again this difference is statistically significant so you can feel confident more employees like learning statistics than doing annual performance reviews (of course!).
5. 1-Proportion Test
Use the 1-proportion test to see if an observed proportion from binary data is different than what you would expect from chance. This is ideal for testing preference data. If you provide two options to consumers, there’s a 50/50 chance they’d select either one. Test the observed proportion against the chance proportion of .5.
For example, if 9 out of 10 respondents prefer Design A over Design B, is that difference statistically significant? To find out you test .90 (9/10) against the proportion you expect if there was no preference (.50). I plugged the values in the online calculator shown below.
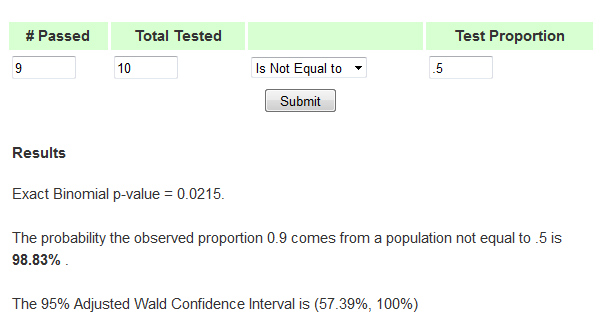
The online calculator generates a p-value of .0215. Even with a small sample size of just 10 respondents, you’d only expect to see that much deviation from .50 about 2% of the time. That’s low enough that it’s statistically significant and you can say Design A is preferred.
Summary
When you’re ready to analyze your data, you have several tests to choose from. The right one depends on the type of data you have as well as your goal and the results you’re looking for:
- The Adjusted Wald confidence interval works when you’re looking at binary data.
- A t-distribution confidence interval is best with continuous data.
- A 2-sample t-test is for when you have two sets of continuous data.
- A 2-proportion test works when you have data covering two different proportions.
- A 1-proportion test is optimal when you’re testing preference data.


