 Statistically significant.
Statistically significant.
It’s a phrase that’s packed with both meaning, and syllables. It’s hard to say and harder to understand.
Yet it’s one of the most common phrases heard when dealing with quantitative methods.
While the phrase statistically significant represents the result of a rational exercise with numbers, it has a way of evoking as much emotion. Bewilderment, resentment, confusion and even arrogance (for those in the know).
I’ve unpacked the most important concepts to help you the next time you hear the phrase.
Not Due to Chance
In principle, a statistically significant result (usually a difference) is a result that’s not attributed to chance.
More technically, it means that if the Null Hypothesis is true (which means there really is no difference), there’s a low probability of getting a result that large or larger.
Statisticians get really picky about the definition of statistical significance, and use confusing jargon to build a complicated definition. While it’s important to be clear on what statistical significance means technically, it’s just as important to be clear on what it means practically.
Consider these two important factors.
- Sampling Error. There’s always a chance that the differences we observe when measuring a sample of users is just the result of random noise; chance fluctuations; happenstance.
- Probability; never certainty. Statistics is about probability; you cannot buy 100% certainty. Statistics is about managing risk. Can we live with a 10-percent likelihood that our decision is wrong? A 5-percent likelihood? 33 percent? The answer depends on context: what does it cost to increase the probability of making the right choice, and what is the consequence (or potential consequence) of making the wrong choice? Most publications suggest a cutoff of 5%—it’s okay to be fooled by randomness 1 time out of 20. That’s a reasonably high standard, and it may match your circumstances. It could just as easily be overkill, or it could expose you to far more risk than you can afford.
What it Means in Practice
Let’s look at a common scenario of A/B testing with, say, 435 users. During a week, they are randomly served either website landing page A or website landing page B.
- 18 out of 220 users (8%) clicked through on landing page A.
- 6 out of 215 (3%) clicked through on landing page B.
Do we have evidence that future users will click on landing page A more often than on landing page B? Can we reliably attribute the 5-percentage-point difference in click-through rates to the effectiveness of one landing page over the other, or is this random noise?
How Do We Get Statistical Significance?
The test we use to detect statistical difference depends on our metric type and on whether we’re comparing the same users (within subjects) or different users (between subjects) on the designs. To compare two conversion rates in an A/B test, as we’re doing here, we use a test of two proportions on different users (between subjects). These can be computed using the online calculator or downloadable Excel calculator.
Below is a screenshot of the results using the A/B test calculator
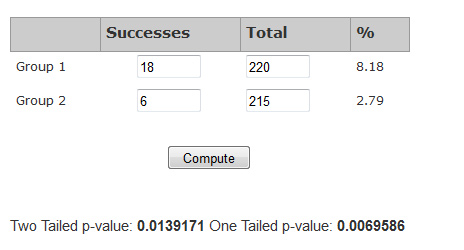
To determine whether the observed difference is statistically significant, we look at two outputs of our statistical test:
- P-value: The primary output of statistical tests is the p-value (probability value). It indicates the probability of observing the difference if no difference exists. The p-value from our example, 0.014, indicates that we’d expect to see a meaningless (random) difference of 5% or more only about 14 times in 1000. If we are comfortable with that level of chance (something we must consider before running the test) then we declare the observed difference to be statistically significant. In most cases, this would be declared a statistically significant result.
- CI around Difference: A confidence interval around a difference that does not cross zero also indicates statistical significance. The graph below shows the 95% confidence interval around the difference between the proportions outputted from the stats package. The observed difference was 5% (8% minus 3%) but we can expect that difference itself to fluctuate. The CI around the difference tells us that it will most likely fluctuate between about 1% and 10% in favor of Landing Page A. But because the difference is greater than 0%, we can conclude that the difference is statistically significant (not due to chance). If the interval crossed zero—if it went, for example, from -2% to 7%—we could not be 95% confident that the difference is nonzero, or even, in fact, that it favors Landing Page A.
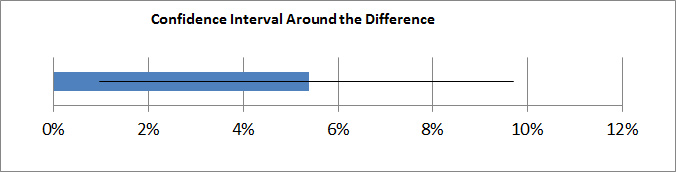
Figure 1: The blue bar shows 5% difference. The black line shows the boundaries of the 95% confidence interval around the difference. Because the lower boundary is above 0%, we can also be 95% confident the difference is AT LEAST 0–another indication of statistical significance.The boundaries of this confidence interval around the difference also provide a way to see what the upper and lower bounds of the improvement could be if we were to go with landing page A. Many organizations want to change designs, for example, only if the conversion-rate increase exceeds some minimum threshold—say 5%. In this example, we can be only 95% confident that the minimum increase is 1%, not 5%.
What it Doesn’t Mean
Statistical significance does not mean practical significance.
The word “significance” in everyday usage connotes consequence and noteworthiness.
Just because you get a low p-value and conclude a difference is statistically significant, doesn’t mean the difference will automatically be important. It’s an unfortunate consequence of the words Sir Ronald Fisher used when describing the method of statistical testing.
To declare practical significance, we need to determine whether the size of the difference is meaningful. In our conversion example, one landing page is generating more than twice as many conversions as the other. This is a relatively large difference for A/B testing, so in most cases, this statistical difference has practical significance as well. The lower boundary of the confidence interval around the difference also leads us to expect at LEAST a 1% improvement. Whether that’s enough to have a practical (or a meaningful) impact on sales or website experience depends on the context.
Sample Size
As we might expect, the likelihood of obtaining statistically significant results increases as our sample size increases. For example, in analyzing the conversion rates of a high-traffic ecommerce website, two-thirds of users saw the current ad that was being tested and the other third saw the new ad.
- 13 out of 3,135,760 (0.0004%) clicked through on the current ad
- 10 out of 1,041,515 (0.0010%) clicked through on the new ad
The difference in conversion rates is statistically significant (p = 0.039) but, at 0.0006%, tiny, and likely of no practical significance. However, since the new ad now exists, and since a modest increase is better than none, we might as well use it (oh and just in case you thought a lot of people clicked on ads, let this remind you of how they don’t!)
Conversely, small sample sizes (say fewer than 50 users) make it harder to find statistical significance; but when we do find statistical significance with small sample sizes, the differences are large and more likely to drive action.
Some standardized methods express differences, called effect sizes, which help us interpret the size of the difference. Here, too, the context determines whether the difference warrants action.
Conclusion and Summary
Here’s a recap of statistical significance:
- Statistically significant means a result is unlikely due to chance
- The p-value is the probability of obtaining the difference we saw from a sample (or a larger one) if there really isn’t a difference for all users.
- A conventional (and arbitrary) threshold for declaring statistical significance is a p-value of less than 0.05.
- Statistical significance doesn’t mean practical significance. Only by considering context can we determine whether a difference is practically significant; that is, whether it requires action.
- The confidence interval around the difference also indicates statistical significance if the interval does not cross zero. It also provides likely boundaries for any improvement to aide in determining if a difference really is noteworthy.
- With large sample sizes, you’re virtually certain to see statistically significant results, in such situations it’s important to interpret the size of the difference.
- Small sample sizes often do not yield statistical significance; when they do, the differences themselves tend also to be practically significant; that is, meaningful enough to warrant action.
Now say statistically significant three times fast.


