Questioning the effectiveness of usability testing may sound like a relic from the past.
Questioning the effectiveness of usability testing may sound like a relic from the past.
In the early years of industrial usability engineering, there was a constant need to justify the activity of (and your job in) usability testing. The book Cost-Justifying Usability (Bias & Mayhew, 2005) speaks to this.
Usability testing has since gained significant adoption in organizations. But that doesn’t mean some of the core questions asked decades ago have been answered adequately or should not continue to be asked.
The widespread use of usability testing is evidence that practitioners believe that usability testing is effective. Unfortunately, there are fields in which practitioners’ belief in the effectiveness of their methods does not appear to be warranted for those outside the field (e.g., the use of projective techniques such as the Rorschach test in psychotherapy).
Although usability testing is widely used, might it actually be ineffective, and might practitioners who use it just be fooling themselves? How do we even define and measure the effectiveness of usability testing?
In this article, we examine two core assessments of effectiveness: the reliability of observing usability problems and the success of using usability testing to generate more usable (better) products.
Problems with Observing Problems
Many researchers proclaim the importance of observing behavior over using self-reported data. But observing people using an interface isn’t an objective action like taking someone’s temperature (which itself is prone to variables that affect its reliability, such as the doctor’s experience, the device used, and the location measured). When trying to identify critical events like usability problems from observations of user behavior, there is strong evidence that what you get is what you see, and not everyone sees the same things. For a method to be valid (a type of effectiveness), it needs to be reliable.
Since 1998 several papers have questioned the reliability of observing usability problems. The common finding in these studies, which include the famous Comparative Usability Evaluation (CUE) studies, was that observers (either individually or in teams across usability laboratories) who evaluated the same product produced markedly different sets of discovered problems. For example:
- CUE-1 – Four teams evaluated a calendar app; they reported 141 problems but found only 1 in common. Molich et al. (1998) had four independent usability laboratories carry out inexpensive usability tests of a software application for new users. The four teams were free to use their own methods and reported 141 different problems, with only one problem common among all four teams. The average any-2 agreement between teams was just 4%. Molich et al. (1998) attributed this inconsistency to variability in the approaches taken by the teams (task scenarios, level of problem reporting).
- CUE Replication – Six teams tested a dialog box; no problems were detected by all teams. Kessner et al. (2001) had six professional usability teams, who were also free to use their own methods, independently test an early prototype of a dialog box. None of the problems were detected by every team, and 18 problems were described by one team only.
- CUE-2 – Nine teams evaluated Microsoft Hotmail; 232 problems were unique. Molich et al. (2004) assessed the consistency of usability testing across nine independent organizations that evaluated the same website. They documented considerable variability in methodologies, resources applied, and problems reported. The total number of reported problems was 310, with only two problems reported by six or more organizations, and 232 problems (61%) uniquely reported. The average any-2 agreement between teams was 7%.
- CUE-4 – Seventeen teams evaluated the Hotel Pennsylvania website using either usability testing or expert review with low problem overlap. Molich and Dumas (2008) had a method and outcomes similar to the previous CUE studies, but with nine teams conducting usability testing and eight teams performing expert reviews. The average any-2-agreement was 11% for the teams that used expert review and 17% for usability testing.
- CUE-9 – Nineteen teams evaluated the U-Haul website with stronger control over what observers reviewed. Hertzum et al. (2014) published results from CUE-9, in which 19 experienced usability professionals analyzed videos of test sessions with five users who worked on reservation tasks at a truck rental website. Nine professionals analyzed moderated sessions (average any-2 agreement was 31%); ten analyzed unmoderated sessions (average any-2 agreement was 30%). Even with evaluators watching the same videos, there was still relatively low overlap among the usability professionals’ problem lists.
Is It Realistic to Expect Consistency in Usability Problem Discovery?
The CUE-type studies (which are now up to CUE-10) are important but disturbing research. If we advocate for the importance of observation but the observations themselves are unreliable, how can usability testing be effective?
There is a clear need for more research in this area to reconcile these studies with the implied understanding that usability testing improves products.
For example, a limitation of research that stops after comparing problem lists is that it isn’t possible to measure usability improvement (if any) that would result from product redesigns derived from those problem lists.
Additionally, when comparing problem lists from many evaluators, one aberrant set of results can have an extreme effect on measurements of consistency across labs. The more evaluators involved, the more problems get uncovered and the more likely one evaluator will see an uncommon problem (matching the large problem sets also exacerbates the disagreement). For example, with CUE-4 there were 86 different experiences observed from 17 teams (76 test participants and 10 expert reviewers) with mostly different tasks. The low overlap in problems is largely a function of the 86 different experiences which increased the number of low frequency (hard-to-discover) problems and reduced the consequent overlap (something Molich and Dumas also felt was a contributing factor).
CUE-4 was a relatively uncontrolled study, allowing the participating groups to define their own tasks and apply their own methods. Even when these variables are controlled, as in CUE-9, the problem lists of observers watching the same behaviors improved but didn’t match exactly. In our meta-analysis, we’ve found the overlap among problem lists from controlled studies (~59% any-2 agreement), while less than 100%, does tend to be considerably higher than those from uncontrolled studies (~17% any-2 agreement).
Is Iterative Design and Usability Testing Effective?
Interpreting these CUE-type studies as being indicative of a lack of reliability starkly contrasts with published studies in which iterative usability tests (sometimes in combination with other UCD methods) have led to significantly improved products. For example,
- A tutorial for first-time computer users required substantial redesign in its first iteration, none in its final iteration. Al-Awar et al. (1981) may be the earliest publication that describes rapid iteration of design and evaluation, reporting substantial improvement across multiple iterations of a tutorial for first-time computer users, ending when there was no need for any redesign with the last group of participants.
- Usability testing of automated training for IBM office computers revealed numerous issues in the first iteration, none in the final iteration. Using an approach modeled on Al-Awar et al., Kennedy (1982) reported success after applying iterative design and evaluation to the operator training procedures for the IBM System/23, a computer designed to be easy for office workers to use.
- Participants had 100% task completion rates following multiple design iterations using a natural language voice recognition calendar. Kelley (1984) used design iteration to improve an early natural language voice recognition calendar application (one of the first published applications of the Wizard of Oz, or WoZ, method in voice user interface design). In the first phase, he had 15 participants complete tasks with the system, making design changes as indicated throughout the phase rather than waiting until the end. He then validated the final design with an additional six participants who successfully completed the tasks without additional redesign, making this an early example of RITE (Rapid Iterative Testing and Evaluation).
- A messaging system for the 1984 Olympics was widely used after multiple design iterations driven by multiple types of evaluations. Gould et al. (1987) applied iterative evaluation to the design of a successful messaging system for the 1984 Olympics. “In evaluating the merits of our principles of design, one must ask if OMS [Olympic Messaging System] was successful. It was. It was reliable and responsive. It ran 24 hours per day for the four weeks the Olympic villages were open. … We worked in the villages everyday and observed that the Olympians liked the system. It was used over 40,000 times during the four-week event. Forty percent of Olympians used it at least once. It was used an average of 1–2 times per minute, 24 hours per day” (p. 761).
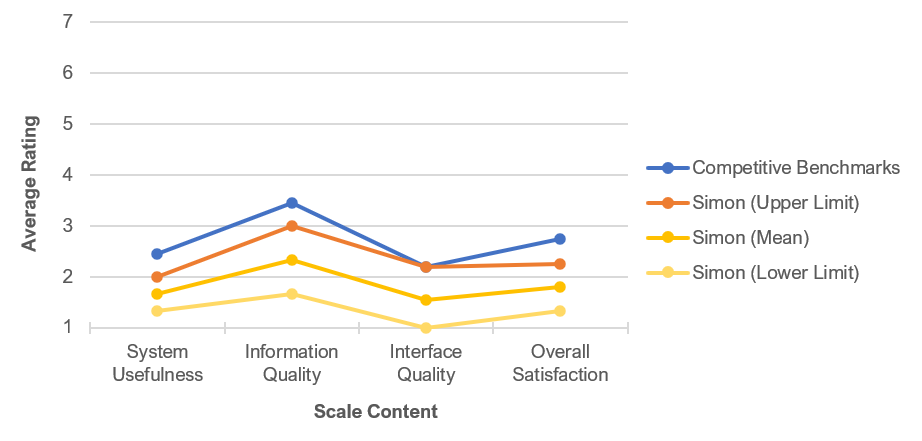
- Iterative testing and redesign of the Simon personal communicator improved objective and subjective usability metrics beyond its planned benchmarks. Lewis (1996) used multiple design iterations in the development of the Simon personal communicator, recipient of numerous industry product awards and now widely regarded as the first commercially available smartphone. “As a consequence of this process of iterative problem identification and design improvement, each iteration showed significant improvement in both user performance and satisfaction. … As Figure 1 shows [reproduced below], Simon significantly exceeded its benchmarks for all PSSUQ … A lower PSSUQ score is better than a higher one” (p. 764).
Figure 1: PSSUQ scale scores for Simon and competition. (Lower is better.)
Investigating Effectiveness of Iterative Design and Usability Testing with Designed Experiments
The papers referenced above are case studies, but there are two papers from the early 1990s that describe designed experiments.
- Usability testing and heuristic evaluation both led to better experiences. One of the most notable papers is by Bailey et al. (1992). They compared two user interfaces derived from the same base interface: one modified via heuristic evaluation and the other modified via iterative usability testing (three iterations, five participants per iteration). They conducted this experiment with two interfaces, one character-based and the other a graphical user interface (GUI), with the same basic outcomes. The number of changes indicated by usability testing was much smaller than the number indicated by heuristic evaluation, but user performance was the same with both final versions of the interface. All designs after the first iteration produced faster performance and, for the character-based interface, were preferred to the original design. The time to complete the performance testing was about the same as the time required for the completion of multi-reviewer heuristic evaluations.
- Task metrics improved across iterations. Bailey (1993) provided additional experimental evidence that iterative design based on usability tests leads to measurable improvements in the usability of an application. The participants in the experiment were eight designers, four with at least four years of professional experience in interface design and four with at least five years of professional experience in computer programming. All designers used a prototyping tool to create a recipe application (eight applications in all). In the first wave of testing, Bailey videotaped participants performing tasks with the prototypes, three different participants per prototype. Each designer reviewed the videotapes of the people using his or her prototype and used the observations to redesign his or her application. This process continued until each designer indicated that it was not possible to improve his or her application; all stopped after three to five iterations. Comparison of the first and last iterations indicated significant improvement in measurements such as number of tasks completed, task completion times, and repeated serious errors.
Summary and Discussion
The results of the CUE-type studies show that usability practitioners must conduct their usability tests as carefully as possible, document their methods completely, and show proper caution when interpreting their results. But even when evaluators are observing videos of the same users (completely controlled) there will be disagreement on what the usability problems are.
Agreement isn’t necessarily the key goal of iterative design and small sample assessment. The ultimate goal is improved usability and a better user experience, and there may be many paths via iteration to that goal.
The limitations of usability testing make it insufficient for certain testing goals, such as quality assurance of safety-critical systems. It can be difficult to assess complex systems with complex goals and tasks. On the other hand, as Landauer (1997, p. 204) stated over 20 years ago: “There is ample evidence that expanded task analysis and formative evaluation can, and almost always do, bring substantial improvements in the effectiveness and desirability of systems.”
Is usability testing effective? In short, yes, when the focus is on downstream improvement in user performance and experience. Usability testing appears to be effective despite the reliability issues associated with problem lists based on observed behavior (physical and verbal). It would be helpful, though, to have more than just two designed experiments investigating how iterative design and evaluation does what it does (something we hope to tackle in some upcoming research).