The standard deviation is the most common way of measuring variability or “dispersion” in data. The more the data is dispersed, the more measures such as the mean will fluctuate from sample to sample.

That means higher variability (higher standard deviations) requires larger sample sizes. But exactly how much do standard deviations—whether large or small—impact the sample size?

Variability is one of four factors that affect sample size estimation. In previous articles, we’ve discussed key components of sample size estimation formulas for confidence intervals, benchmark tests, and mean differences, including:

• Precision: This is the desired margin of error for confidence intervals or the size of the difference in comparisons (the smallest difference that you need to be able to detect). The more precision you need, the larger the required sample size.
• Confidence: This is the value from the t distribution that matches the desired level of confidence for confidence intervals and corresponds to the alpha criterion (control of Type I errors) for comparisons. The more confidence you need, the larger the required sample size.
• Power: Power does not play a role in sample size estimation for confidence intervals, but for comparisons, this is the value from the t distribution that matches the desired level of power for the test and corresponds to the beta criterion (control of Type II errors). The more power you need, the larger the required sample size.
• Variability: As discussed above, variability refers to the extent to which a set of values tends to be close to one another or spread out, typically measured with the standard deviation. The larger the standard deviation, the larger the required sample size.

Researchers planning studies have some control over precision, confidence, and power but little control over the standard deviation of measurements. The exception to this is when two metrics measure the same property but differ in their standard deviations, so researchers can exercise some control over the standard deviation through the metric they select.

In this article, we describe how changes in standard deviation affect sample size requirements.

A Little Math (Really, Just a Little)

To understand how changes in the standard deviation affect sample sizes we need to refer to the core sample size formula we use for confidence intervals.

In the equation below, n is the estimated sample size, s is the standard deviation, t is the t-value for the desired level of confidence, and d is the targeted size for the interval’s margin of error.

Consider the following basic sample size formula for confidence intervals:

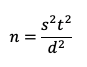
In the next formula, we multiplied s by a constant (c) to represent a change in the standard deviation.

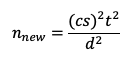
Next, because (cs)² = c²s²:

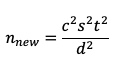
Finally, because n = (s²t²)/d² (as shown in the first equation):

So, when the standard deviation changes by the factor of c, the new sample size estimation will be the square of c times the original sample size estimate.

We don’t show the derivations here, but you get the same result for other similar sample size estimation equations for benchmark tests and assessments of mean differences (all of which have s² as a factor in their numerators, including iterative methods), specifically:

• When c = 1 (no change in the standard deviation), n_new and n will be the same.
• When c < 1 (new standard deviation is smaller), n_new will be smaller than n.
• When c > 1 (new standard deviation is larger), n_new will be larger than n.

Some Examples

To illustrate how this works, here are a few examples from UX research and practice.

Example 1: Effect of Increasing the Standard Deviation

We’ve done a lot of research on the System Usability Scale (SUS), a measure of perceived usability that can range from 0 to 100. In 2011, we published A Practical Guide to the System Usability Scale, which included information about the standard deviation of the SUS from the best sources available at that time.

Across sources and different types of products, we found estimates of the standard deviation ranged from about 16.8 to 22.5 (averaging 21.4), including estimates from retrospective UX surveys for business software (s = 16.8) and consumer software (s = 17.6).

Suppose you’re planning to conduct a retrospective UX survey of business software where you want to compute 95% confidence intervals around your mean SUS scores (so t will be about equal to 2), want the margin of error to be no more than ±5 points, and use the historical estimate of the standard deviation in this research context (s = 16.8). The basic sample size estimate would be:

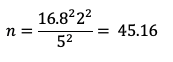
Suppose you then decide to expand the context of the research to include other types of products and services. From the historical data, you know this will increase the variability of the data, probably somewhere between 18 and 22.5.

To get from 16.8 to 18, the value of the constant (c) is 18/16.8 = 1.0714 (an increase of 7.14%). From 16.8 to 20 it’s 20/16.8 = 1.1905 (an increase of 19.05%), and from 16.8 to 22.5 it’s 22.5/16.8 = 1.3393 (an increase of 33.93%). The resulting new sample size estimates would be:

• s = 18: n = 45.16(1.0714²) = 45.16(1.148) = 51.84 (an increase of about 15%)
• s = 20: n = 45.16(1.1905²) = 45.16(1.417) = 64.0 (an increase of about 42%)
• s = 22.5: n = 45.16(1.3393²) = 45.16(1.7937) = 81.0 (an increase of about 79%)

Because c is squared, relatively modest increases in standard deviation can correspond to large increases in sample size estimates.

Example 2: Effect of Decreasing the Standard Deviation

In a previous article, we reported that aggregated data from over 100,000 responses for hundreds of five-, seven-, and eleven-point rating scales revealed a common pattern. The average standard deviation across over 4,000 scale instances was about 25% of the maximum range of the rating scale (e.g., 25 for item scores rescaled to 0–100 points).

We followed that research with an investigation of the variability and reliability of standardized UX scales made up of multiple items (from 2 for the UX-Lite to 16 for the CSUQ). We found, as expected from psychometric theory, that multi-item questionnaires have lower variability than single UX items, with a typical standard deviation of about 19% of the maximum scale range (e.g., 19 for questionnaire scores rescaled to 0–100 points).

Suppose in a retrospective survey of consumer software products you’re planning to collect a simple single-item measure of perceived usability that, after interpolation to 0-100 points, has a historical standard deviation of 25. Using the criteria from Example 1, you want to compute 95% confidence intervals around your mean scores (so t will be about equal to 2) and want the margin of error to be no more than ±5 points.

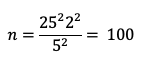
Because it has a lower historical standard deviation of 17.6, you want to consider replacing this single-item metric with the ten-item SUS. In this case, the value of c is less than 1 (17.6/25 = 0.704, a decrease of about 30%). The new sample size estimate is:

• s = 17.6: n = 100(0.704²) = 100(0.4956) = 49.56 (a decrease of about 50%)

Again, because c is squared, the 30% decrease in standard deviation led to a 50% decrease in the sample size estimate. The decrease in estimated sample size is desirable, but survey respondents will have to answer ten questions instead of one to provide a measure of perceived usability, so making the final decision will also depend on the cost of additional respondents and the potential impact of adding nine more items to the length of the survey.

A Useful Table

Table 1 shows how increases and decreases in standard deviations affect sample size estimates in descending order from a 50% increase in standard deviation to a 50% decrease.

% change in s	c	Change in n (c2)	Change in n (±%)
50%	1.50	2.25	+125%
40%	1.40	1.96	+96%
30%	1.30	1.69	+69%
20%	1.20	1.44	+44%
10%	1.10	1.21	+21%
5%	1.05	1.10	+10%
0%	1.00	1.00	0%
−5%	0.95	0.90	−10%
−10%	0.90	0.81	−19%
−20%	0.80	0.64	−36%
−30%	0.70	0.49	−51%
−40%	0.40	0.36	−64%
−50%	0.50	0.25	−75%

Table 1: Effect of changes in standard deviation (s) on sample size estimates (n). To compute a new n that increases or decreases by the specified percentage change, multiply the initial estimate by c².

At the extremes in the table, if an initial sample size estimate was 100, then a 50% increase in standard deviation would more than double the estimate to 225 (100 × 2.25). On the other hand, if the initial estimate was 100 and the standard deviation was cut in half (50% decrease), then the new estimate would be a sample size of 25 (100 × 0.25).

In Example 1, the change in standard deviation from 16.8 to 20 was 19% (just under 20%). For the example, we estimated an increase in sample size of 42%, which would be 1.42 times the original sample size, consistent with the table’s values of c² = 1.44 (change of +44%) for a 20% increase in standard deviation.

In Example 2, the change in standard deviation from 25 to 17.6 was a decrease of about 30%, for which the sample size estimate dropped by about 50%, consistent with the values shown in the table (c² = 0.49, % change of −51%).

The magnitudes of standard deviations in these examples are consistent with what we’ve seen in practice.

For a more comprehensive analysis, we examined UX-Lite scores from 220 studies with a combined sample size of just over 9,000 (ranging from a minimum of n = 10 for the smallest study and n = 116 for the largest one). The median (50^th percentile) in this distribution of standard deviations was 19.3, with the following standard deviations at key percentiles (showing the percentage change from the median in parentheses):

• 1^st percentile: 11.9 (−38%)
• 5^th percentile: 13.6 (−30%)
• 10^th percentile: 14.6 (−24%)
• 25^th percentile: 16.6 (−14%)
• 75^th percentile: 21.2 (+10%)
• 90^th percentile: 22.9 (+19%)
• 95^th percentile: 24.5 (+27%)
• 99^th percentile: 28.4 (+48%)

For comparison with a typical (50^th percentile) standard deviation of the UX-Lite based on data from 220 studies and total n = 9,029, the percentage change in standard deviation associated with the interquartile range (25^th to 75^th percentiles) went from −14% to +10%, and for the 90% range (from 5^th to 95^th percentiles) went from −30% to +27%.

Comparisons of the extremes with each other were even larger. For example, from the 99^th percentile of 28.4 to the 1^st percentile of 11.9, c = 28.4/11.9 = .42, a decrease of about 58%.

Thus, we expect 50% changes in standard deviation to be rare (but possible). As shown in our real-world examples, it’s plausible to be confronted with differences as large as 35%.

It’s also important to keep in mind that our examples are based on very large datasets, so we have pretty accurate estimates of the typical standard deviations for well-known metrics like SUS and UX-Lite. These large sets of data also show, however, that there can be a lot of variability in estimates of standard deviations when sample sizes are smaller. When a historical standard deviation is not based on a substantial set of data, it will usually be better practice to overestimate than underestimate the standard deviation when computing sample size requirements (e.g., you might inflate the standard deviation by 5 or 10% as long as your budget can handle the increase in participant cost).

Summary

So, how do changes in standard deviation affect sample size estimation? Even somewhat modest changes to standard deviations can have large effects on sample size estimation.

When planning sample sizes for quantitative research, standard deviations matter. Because there is a squared relationship between changes in standard deviations and resulting sample size estimates, the effects are amplified, as shown in Table 1. When standard deviations increase by 50%, the sample size is roughly doubled; when they decrease by 50%, the new sample size is a quarter of the original.

When all other research considerations are the same and you have a choice, choose metrics with lower standard deviations. When there is no compelling reason to do otherwise, research is more efficient with metrics that have smaller standard deviations.

When all other research considerations are not the same, choosing the right metric can be trickier. Unfortunately, in research planning, considerations are not always the same. For example, one way to reduce standard deviations is to measure constructs with multi-item questionnaires (e.g., SUS), but in lengthy surveys adding additional items can increase the length of a survey and potentially increase the dropout rate. One of the variable expenses in research is the cost per participant, which influences how important it is to minimize sample size requirements.

The accuracy of historical standard deviations depends on the amount of data available to estimate them. You can be reasonably confident when your historical sample size was computed from hundreds of studies and thousands of individual cases, but be cautious when your historical standard deviations are based on a small number of studies. (Consider inflating them by 5% or 10% as long as the cost of additional participants isn’t too high.)