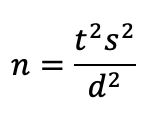Despite its age and the availability of other UX measures such as the UX-Lite™ and SUPR-Q®, the ten-item System Usability Scale (SUS) is still a very popular measure. It’s used widely in benchmark tests of software products to generate an overall score of perceived usability.
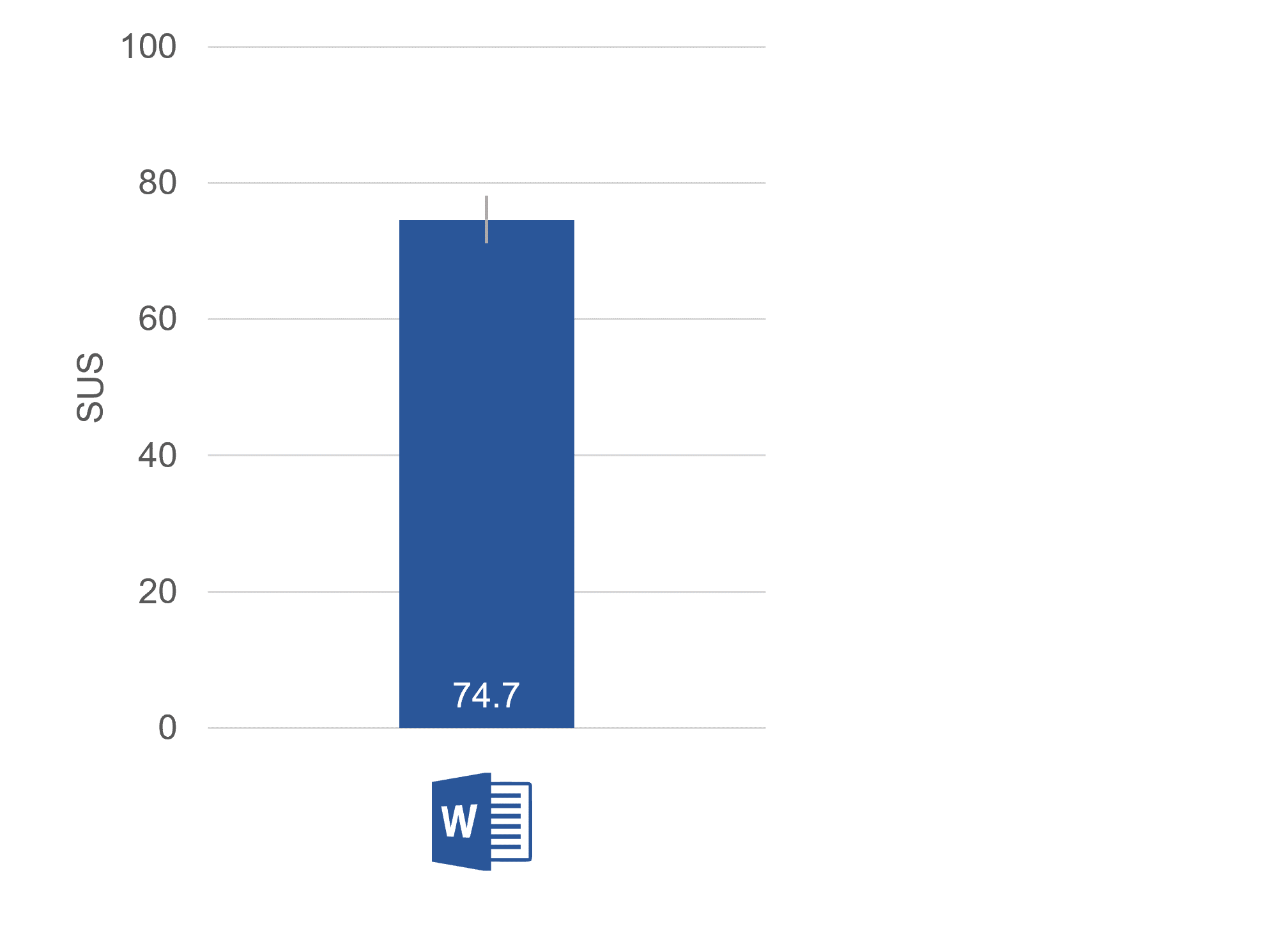
We regularly collect SUS scores for dozens of consumer and business products to publish in our UX benchmark reports. For example, in our 2020 benchmark report, Microsoft Word received a SUS score of about 75 (74.7 ± 3.5—see Figure 1).
We’re often asked how large the sample size needs to be for UX research using the SUS.
The short (unsatisfying) answer is “it depends.” But fortunately, there is a way to generate a more precise answer, starting with what you are trying to do with the SUS score. There are three primary goals with metrics like the SUS:
- Stand-Alone Estimate/Confidence Interval: Estimate the SUS for a population from one sample.
- Comparison to a Benchmark: Determine whether a SUS score exceeds a benchmark (such as 68, the average score).
- Comparison to Another Sample: Compare SUS scores for comparable products or the same product over time.
When the goal is to compute a SUS score from a sample of users (#1 from above), the sample size calculation is based on how precise you need your estimate to be. That precision is described using a confidence interval. The SUS score of 74.7 for Microsoft Word came from 111 users. It has a margin of error of ±3.5 points with 95% confidence, so the confidence interval ranges from 71.2 to 78.2.
With larger sample sizes you have a more precise estimate (narrower confidence intervals) for whatever product experience you are measuring. Smaller sample sizes give you a less precise estimate (wider confidence interval).
The sample size calculations are based on working backward from the width of the confidence interval (which we cover in this article). To compute the sample size, it’s a matter of trading off your desired level of precision against the cost of additional samples. (We’ll cover the computations for goals #2 and #3 in upcoming articles.)
What Drives Sample Size Requirements for Confidence Intervals?
A confidence interval is the most common way to express the precision of a metric collected from a sample. It’s derived from the more familiar margin of error—something you likely have seen reported for polls accompanied with a ±; for example, a margin of error of ±5%. Margins of errors can be expressed as percentages or as the appropriate units of measure (±10%, ±7 SUS points, ±1,000 pounds, ±1.8B$).
As shown in Figure 2, the three things you need to know to compute your sample size for a confidence interval are
- An estimate of the SUS standard deviation: s
- The level of confidence (typically 90% or 95%): t
- The desired margin of error around your estimate (using points or percentages): d
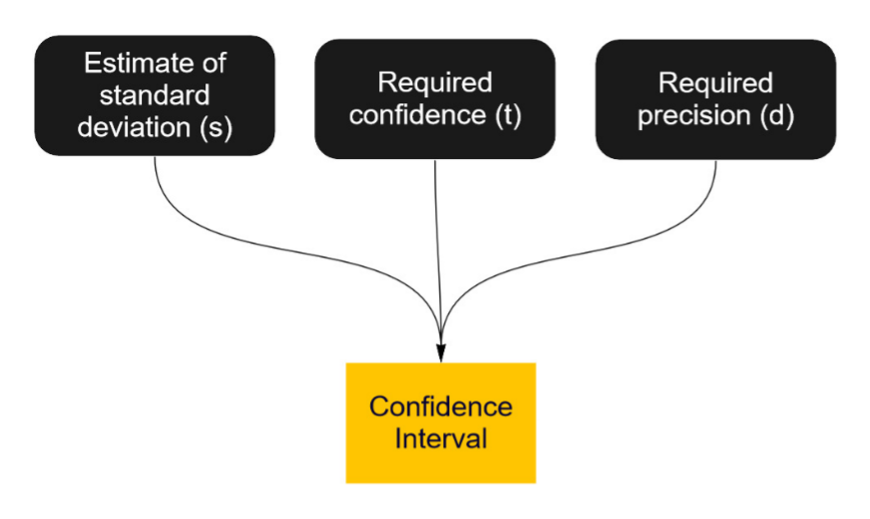
With those ingredients, you have what you need to generate a sample size for a confidence interval. In our book Quantifying the User Experience, we devote Chapter 6 to sample size estimation, including the derivation of all the formulas needed for the major types of sample size estimation.
Skipping most of the math for this article, the basic sample size formula for confidence intervals is
where s is the standard deviation (s2 is the variance), t is the t-value for the desired level of confidence, and d is the targeted size for the interval’s margin of error (i.e., precision).
Now we’ll walk you through how to get these values.
1. An Estimate of the Standard Deviation of the SUS
The first ingredient is a measure of variability (the standard deviation) for the specific product and users you intend to measure. This can seem quite puzzling if you’re new to sample size calculations. If you had the standard deviation for this product and group of users, then why would you need to collect a sample to estimate SUS?
Fortunately, the benefit of using a standardized and well-known measure such as the SUS is that we have lots of data for lots of products. So, while it’s unlikely to be exactly the same for the specific product and user context you’re evaluating, it’s probably close enough to provide a useful sample size estimate.
In 2011, we published A Practical Guide to the System Usability Scale, which includes information about the standard deviation of the SUS from the best sources available at that time. Across sources and different types of products, estimates of the standard deviation ranged from about 16.8 to 22.5 (averaging 21.4), including estimates from retrospective UX surveys for business software (s = 16.8) and consumer software (s = 17.6).
Our most recent sources for estimating the standard deviation of the SUS are from retrospective SUS surveys that we conducted on business and consumer software in 2017 and 2020 (Table 1).
| SUS | 2017 | 2020 |
| Business | 18.1 | 16.9 |
| Consumer | 17.7 | 17.9 |
Table 1: Standard deviations for the SUS in our 2017 and 2020 surveys.
Across these measurements of the standard deviation, the average is about 17.7. This is reasonably consistent with the average of the corresponding estimates from 2011 (17.2).
2. The Confidence Level
While not always explicitly stated, polls with margins of error have specific confidence levels. Typically, these are set to 95% or 90% but can be any value (in practice, usually ≥ 80% but never 100%). The sample size formula doesn’t use the confidence level value (e.g., 95%). Instead, it uses a standard score derived from the normal (Z) and t-distributions that correspond to the desired level of confidence. This value is usually close to 2 for 95% confidence.
Technical Note: Using t in this process introduces a complication. The value of t depends on its degrees of freedom (df), which in turn depends on the sample size—which is what we’re trying to compute. We get around this by starting with a z-value, which is not dependent on df, to get the initial estimate of n, then iterating until we settle on the final value. (For details, see Quantifying the User Experience.)
3. The Desired Margin of Error
This takes us to the final and most influential part of the formula: the desired margin of error (d), which makes up half the confidence interval. Of the things you might desire, the margin of error might not top the list. But for sample size planning, the desired margin of error is how much uncertainty you can tolerate in your estimate.
Of course, an ideal amount of uncertainty would be 0 or very low, but the price to pay is a very large sample size. So for this step, you need to work with realistic values and assess the feasibility of the sample size you would need to achieve that level of precision. For SUS, a good place to start would be a margin of error of ±5. A SUS score of 75 with a margin of error of ±5 points would have a confidence interval ranging from 70 to 80. For less precision, you can increase d to 10 (confidence interval from 65 to 85) or, for more precision, decrease d to 2.5 (confidence interval from 72.5 to 77.5).
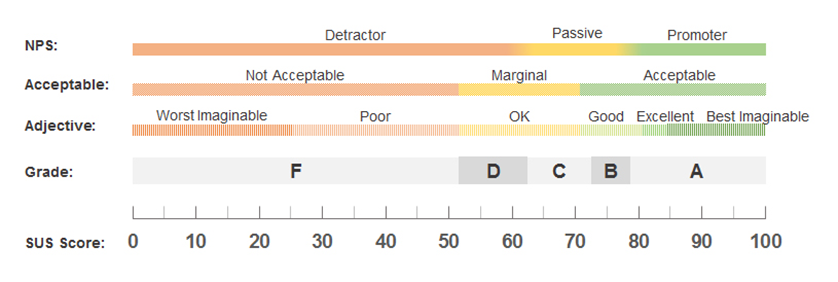
We recommend starting with ±5 points because the ten-point range it creates for a SUS confidence interval can roughly correspond to the letter grades and adjectives used to interpret the SUS, as shown in Figure 3. For example, a low-scoring D ranges from 52 to 63; an average C ranges from 63 to 73; an above-average B ranges from 73 to 79. But even ±10 points (a twenty-point range) can still differentiate between acceptable, marginal, and not acceptable. Of course, it’s likely the SUS score obtained from your sample, while still having a confidence interval less than ten points wide, may cross between grades and adjectives. If you want to increase the likelihood of staying within a grade or adjective range, you’ll need to increase your sample size.
| d | SUS; 90% | SUS; 95% |
|---|---|---|
| 15 | 6 | 8 |
| 10 | 11 | 15 |
| 7.5 | 17 | 24 |
| 5 | 36 | 51 |
| 2.5 | 138 | 195 |
| 2 | 214 | 304 |
| 1 | 850 | 1,206 |
Table 2: Sample size requirements for various SUS confidence intervals (s = 17.7).
For example, if you need the interval to have 90% confidence and precision of ±15, then you need a sample size of only six (a very imprecise estimate). At the other end of the table, if you need 95% confidence and precision of ±1, you’ll need a sample size of 1,206 (a very precise estimate).
You can see a sort of Goldilocks zone for reasonably precise margins of error (d from 2 to 5), which have reasonably attainable sample size requirements (n from 36 to 304). The table also shows how sample size estimates balance statistics and logistics. The math for a high level of precision may indicate aiming for a sample size of 1,000, but the feasibility (cost and time) of obtaining that many participants might be prohibitive, even in a retrospective survey or unmoderated usability study.
What about the Different Estimates for the Standard Deviation of SUS?
As previously mentioned, in A Practical Guide to the System Usability Scale, estimates of the standard deviation of the SUS from different sources ranged from 16.8 to 22.5.
For example, suppose your estimate is 20. Because this estimate is larger than the 17.7 used to build Table 2, you’ll need larger sample sizes to maintain your desired levels of confidence and precision, as shown in Table 3.
| d | SUS; 90% | SUS; 95% |
|---|---|---|
| 15 | 7 | 10 |
| 10 | 13 | 18 |
| 7.5 | 22 | 30 |
| 5 | 46 | 64 |
| 2.5 | 176 | 249 |
| 2 | 273 | 387 |
| 1 | 1,085 | 1,540 |
Table 3: Sample size requirements for various SUS confidence intervals (s = 20).
If your SUS data has a standard deviation close to 17.7, use Table 2. If it’s closer to 20, use Table 3. If it’s in between, then you can use Tables 2 and 3 to get an idea about the approximate sample size. If you need a more precise estimate, see the following technical note.
Technical Note: If you’re working with SUS data that has a very different standard deviation from 17.7 or 20, you can do a quick computation to adjust the values in these tables. The first step is to compute a multiplier by dividing the new target variance (s2) by the variance used to create the table. Then multiply the tabled value of n by the multiplier and round it off to get the revised estimate. For example, if the target standard deviation (s) is 19.1, the target variability (s2) is 364.81. The variability from Table 3 is 400 (202), making the multiplier 364.81/400 = .912. To use this multiplier to adjust the sample size of 249 for 95% confidence and precision of ±2.5 shown in Table 3, multiply 249 by .912 and then round it off to 227.
Summary and Takeaways
What sample size do you need when computing a SUS score? There’s no simple answer. It depends on the goal of your study: Stand-Alone Estimate, Comparison with Benchmark, or Comparison to Another Sample. Each goal requires different elements in the sample size estimation processes.
In this article, we covered how to compute the needed sample size for a stand-alone estimate, which uses a confidence interval to describe the precision of a SUS score. The method needs three ingredients: the confidence level, an estimate of the standard deviation, and desired margin of error. We provided the formula and two tables based on typical confidence levels and typical standard deviation for the SUS in retrospective UX studies (s = 17.7) and a more conservative one (s = 20).
For UX researchers working in contexts where the typical standard deviation of the SUS might be different, we provided a simple way to increase or decrease the tabled sample sizes for larger or smaller standard deviations. Both a Practical Guide to the System Usability Scale and Quantifying the User Experience (Chapter 6) provide thorough details on the computations.
