 Sample size computations can seem like an art. Some assumptions are involved when computing sample sizes, but it should be more math than magic.
Sample size computations can seem like an art. Some assumptions are involved when computing sample sizes, but it should be more math than magic.
A key ingredient needed to cook up a sample size estimate is the standard deviation. You need yeast to make bread, and you need a measure of variability to make an estimate of a sample size. But whether the variability used is a lot or a little will significantly alter your final sample size outcome.
The challenge is that you need some estimate of a population’s standard deviation to compute a sample size. This isn’t a problem for binary data such as completion rates or conversation rates because a nice property of binary proportional data is that the standard deviation is a function of the proportion (if you know the proportion you can compute the standard deviation). Although we don’t usually know what the proportion will be, a general practice is to use the maximum variance of proportional data (at a proportion of .50), which provides useful estimates when the actual proportion is between .30 and .70 (Cochran, 1977 [PDF]).
A less favorable property of binary data is that it’s coarse (it’s 1 or 0, yes or no, purchase or didn’t purchase). That coarseness means you need a larger sample size than when using more continuous measures, such as rating scales or completion times, for the same level of precision (or power when making comparisons).
Consequently, most sample size tables, including the ones we’ve published and the ones we provide to our clients, tend to be conservative—we recommend larger sample sizes than may be necessary when a study is not focused on binary outcomes.
For many research endeavors, means from rating scales (individual or combined into standardized questionnaires) are the primary outcome measure, so having a better way to estimate accurate sample size requirements would provide lower (more efficient) sample size estimates.
As we discussed in our earlier articles, if you have historical data for a scale, you can use that standard deviation to compute more accurate sample sizes.
In a previous article, we reported that aggregated data from over 100,000 responses for hundreds of five-, seven-, and eleven-point rating scales revealed a common pattern. The average standard deviation across over 4,000 scale instances was about 25% of the maximum range of the rating scale (e.g., 1 for a five-point scale, 1.5 for a seven-point scale, 2.5 for an eleven-point scale).
From our analysis of individual five-, seven-, and eleven-point items, we found a good estimate of a less-than-average standard deviation (25th percentile) is about 20% of the range (e.g., .8 points for a five-point scale). We also found 20% of the maximum range to be a reliable average estimate for most multi-item UX questionnaires, based on analysis of the SUPR-Q®, SUS, CSUQ, UMUX, UMUX-Lite, and UX-Lite™.
A more conservative estimate for a more variable standard deviation is the 75th percentile of item variability, which tends to be around 28% of the range of the scale (e.g., 1.12 on a five-point scale). All else being equal, sample size requirements based on these estimates (from 20–28%) will be substantially lower than estimates based on the standard deviation of binomial metrics (which is 50% of the range of the scale when p = .5).
In this article, we use these estimates of the percentage of maximum scale range for rating scales to develop tables that UX researchers can use when planning research that will include computing confidence intervals for rating scales or multi-item questionnaires for which there is no historical data. We also compare these sample size estimates with those computed with maximum variance for binary metrics.
Computing Sample Sizes for Confidence Intervals
A Quick Method
When computing sample sizes for rating scales, it’s best to use the iterative method described in Quantifying the User Experience and our Excel stats package. But without iteration, you can quickly estimate sample sizes for confidence intervals with a simple formula:
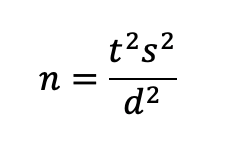
- s is the standard deviation (s2 is the variance), “s” (e.g., typically about 1 on a five-point scale).
- t is the t-value for the desired level of confidence (typically 90% or 95%), usually around 2 for 95% confidence when n ≥ 20 (for values of t with 90% confidence or n < 20, see Table 1).
- d is the planned size for the interval’s margin of error (precision) (e.g., 0.3 on a five-point scale).
| df | 90% | 95% |
|---|---|---|
| 1 | 6.3 | 12.7 |
| 2 | 2.9 | 4.3 |
| 3 | 2.5 | 3.2 |
| 4 | 2.1 | 2.8 |
| 5 | 2.0 | 2.6 |
| 10 | 1.8 | 2.2 |
| 15 | 1.8 | 2.1 |
| 20 | 1.7 | 2.0 |
| 1000 | 1.65 | 1.96 |
Table 1: Approximate two-tailed values of t for different degrees of freedom (df) (for one sample of data,
df = n − 1, for two independent samples, df = n1 + n2 − 2).
For an example with a five-point scale, setting s, the standard deviation, to 1 (25% of the maximum range of 4), setting d, the margin of error, to .2 points (5% of the maximum range), and using 2 for the t-critical value for a 95% confidence level results in a sample size estimate of 100.
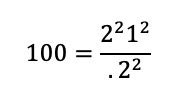
Because 100 > 20, it’s appropriate to use t = 2 for the approximation. However, because we used an approximate value for t, the sample size is slightly different from the estimate of 99 computed using the more complex but more precise iterative method.
Binomial and Rating Scale Sample Size
Table 2 shows the sample sizes needed for a desired margin of error at 95% confidence using the low (20%), medium (25%), and high (28%) estimates for rating scale standard deviations. To standardize this table for different multipoint scales and make it directly comparable to the binomial metric’s range from 0 to 100%, we interpolated the values in the columns for multipoint items to a 0–100-point scale. The interpolation formulas are:
- five-point: y = (x − 1)(100/4)—i.e., subtract 1 from the 5-point rating, then multiply by 25
- seven-point: y = (x − 1)(100/6)—i.e., subtract 1 from the 7-point rating, then multiply by 16.67
- eleven-point: y = x(10)—i.e., multiply the 11-point rating by 10
After this interpolation, the maximum range for a rating scale is 100 (100 − 0), so the estimated standard deviations based on a percentage of the maximum range become, respectively, 20, 25, and 28 points.
The first column of Table 2 shows the desired margin of error (percentages for binary metrics, points for rating scales interpolated to 0–100 points).
The second column shows the sample size needed when using a binary estimate at maximum variance/standard deviation for adjusted-Wald binomial confidence intervals.
The third through fifth columns show the estimated sample sizes for a 0–100-point rating scale for three estimates of its standard deviation. Setting the standard deviation to 25 is the best choice for most planning. When there is a concern that the unknown standard deviation will probably be higher than average, set it to 28. When estimating sample sizes for multi-item questionnaires, it’s best to set the standard deviation to 20.
| Margin of Error (+/−) | Binary Metric, s = 50% | 0–100-Point Rating Scale, s = 20 | 0–100-Point Rating Scale, s = 25 | 0–100-Point Rating Scale, s = 28 |
|---|---|---|---|---|
| 24(%) | 13 | 6 | 7 | 8 |
| 20(%) | 21 | 7 | 9 | 11 |
| 17(%) | 30 | 8 | 11 | 13 |
| 15(%) | 39 | 10 | 14 | 16 |
| 14(%) | 46 | 11 | 15 | 18 |
| 13(%) | 53 | 12 | 17 | 21 |
| 12(%) | 63 | 14 | 20 | 24 |
| 11(%) | 76 | 16 | 23 | 28 |
| 10(%) | 93 | 18 | 27 | 33 |
| 9(%) | 115 | 22 | 33 | 40 |
| 8(%) | 147 | 27 | 40 | 50 |
| 7(%) | 193 | 34 | 52 | 64 |
| 6(%) | 263 | 46 | 70 | 87 |
| 5(%) | 381 | 64 | 99 | 123 |
| 4(%) | 597 | 99 | 153 | 191 |
| 3(%) | 1,064 | 174 | 270 | 338 |
| 2(%) | 2,398 | 387 | 603 | 756 |
| 1(%) | 9,600 | 1,540 | 2,404 | 3,015 |
Table 2: Sample size estimates for binary and rating scale data for 95% confidence.
For example, to obtain a margin of error of ±20 points with 95% confidence, start in the column in Table 2 labeled Margin of Error (+/−) and move down to the row starting 20(%). The column labeled “Binary Metric, s = 50%” is the sample size needed for a binary metric with that margin of error which, assuming maximum variance, would be 21. Using the standard deviation estimates for rating scales would reduce the sample size to 7, 9, or 11 for a low (20% of range), medium (25% of range), or high (28% of range) estimated standard deviation. At this level of precision, the rating scale standard deviations cut the sample size estimate roughly in half!
The savings are even greater for smaller margins of error. For example, at a margin of error of ±2 points, you’d need 2,398 participants using a binary metric. You would need just a quarter of that (603) using the typical rating scale’s standard deviation of 25% of the maximum range.
Table 3 shows the sample sizes needed for 90% confidence, a level commonly used in industrial research. Due to the lower level of confidence, all sample sizes in Table 3 are smaller than their corresponding entries in Table 2, but the ratios of rating scale over binary metric sample sizes are similar (e.g., when s = 25, that ratio is 5/10 = .50 for a margin of error of 24(%), and when the margin of error is 1(%), the ratio is 1693/6762 = .25).
| Margin of Error (+/−) | Binary Metric, s = 50% | 0–100-Point Rating Scale, s = 20 | 0–100-Point Rating Scale, s = 25 | 0–100-Point Rating Scale, s = 28 |
|---|---|---|---|---|
| 24(%) | 10 | 4 | 5 | 6 |
| 20(%) | 15 | 5 | 7 | 8 |
| 17(%) | 21 | 6 | 8 | 10 |
| 15(%) | 28 | 7 | 10 | 12 |
| 14(%) | 32 | 8 | 11 | 13 |
| 13(%) | 38 | 9 | 12 | 15 |
| 12(%) | 45 | 10 | 14 | 17 |
| 11(%) | 54 | 11 | 16 | 20 |
| 10(%) | 65 | 13 | 19 | 24 |
| 9(%) | 81 | 16 | 23 | 29 |
| 8(%) | 103 | 19 | 29 | 36 |
| 7(%) | 136 | 24 | 37 | 46 |
| 6(%) | 186 | 32 | 49 | 61 |
| 5(%) | 268 | 46 | 70 | 87 |
| 4(%) | 421 | 70 | 108 | 135 |
| 3(%) | 749 | 123 | 190 | 238 |
| 2(%) | 1,689 | 273 | 425 | 533 |
| 1(%) | 6,762 | 1,085 | 1,693 | 2,123 |
Table 3: Sample size estimates for binary and rating scale data for 90% confidence.
For example, to achieve a margin of error of ±10 points with 90% confidence, plan on a sample size of 19 for the typical standard deviation of 25, and 13 or 24 for lower (20) and higher (28) estimates of standard deviation. The three sample sizes for the various rating scale standard deviations are, respectively, 20%, 29%, and 37% of the sample needed for a binary metric (n = 65).
We expect these sample size estimates for rating scales to be highly accurate when item means are close to the midpoint and reasonably accurate until means get close to an endpoint. Because the standard deviations for binary metrics and rating scales approach 0 as means approach a scale endpoint, the actual sample size requirements for extreme means will be smaller than those in Tables 2 and 3.
Mapping Margins of Error for 0–100-Point Scales to Five-, Seven-, and Eleven-Point Scales
Interpolation of rating scales to 0–100 points greatly simplifies the comparison of binary and rating scale sample size requirements, and it generalizes its application to any number of scale points from five to eleven. Otherwise, we’d need separate tables for each different multipoint scale. Note that we advise against extrapolating much beyond eleven-point scales when using these tables because we haven’t specifically measured standard deviations for rating scales with more than eleven response options. If you must extrapolate, based on our research and review of the literature, consider using 25% of the maximum range for individual rating scale items and 20% of the maximum range for multi-item questionnaires.
If you or your stakeholders are used to thinking in terms of the original scales, it can be tricky to work backward from the 0–100-point scale. To help with this, Table 4 shows the magnitudes of the margins of error from Tables 2 and 3, rescaled to five, seven, and eleven points.
| 0–100-pt Scale | Five-pt Scale | Seven-pt Scale | Eleven-pt Scale |
|---|---|---|---|
| 24 | 0.960 | 1.440 | 2.400 |
| 20 | 0.800 | 1.200 | 2.000 |
| 17 | 0.680 | 1.020 | 1.700 |
| 15 | 0.600 | 0.900 | 1.500 |
| 14 | 0.560 | 0.840 | 1.400 |
| 13 | 0.520 | 0.780 | 1.300 |
| 12 | 0.480 | 0.720 | 1.200 |
| 11 | 0.440 | 0.660 | 1.100 |
| 10 | 0.400 | 0.600 | 1.000 |
| 9 | 0.360 | 0.540 | 0.900 |
| 8 | 0.320 | 0.480 | 0.800 |
| 7 | 0.280 | 0.420 | 0.700 |
| 6 | 0.240 | 0.360 | 0.600 |
| 5 | 0.200 | 0.300 | 0.500 |
| 4 | 0.160 | 0.240 | 0.400 |
| 3 | 0.120 | 0.180 | 0.300 |
| 2 | 0.080 | 0.120 | 0.200 |
| 1 | 0.040 | 0.060 | 0.100 |
Table 4: Equivalent margins of error for 0–100-point scales with five-, seven-, and eleven-point scales.
The entries in Table 4 were calculated by dividing the margin of error for 0–100-point scales by 100, then multiplying that by the maximum range of the multipoint scale. The maximum range of a five-point scale using the typical response options of 1 to 5 is 4 (5 − 1 = 4), for a seven-point scale is 6 (7 − 1 = 6), and for an eleven-point scale is 10 (10 − 0 = 10).
For example, if you want a margin of error for a five-point scale that is equivalent to ±10 on the 0–100-point scale, you’d use ±0.4. For a seven-point scale, the equivalent margin of error is ±0.6, and for an eleven-point scale is ±1.0. Then, using the typical estimate of the standard deviation for a rating scale from Tables 2 and 3, for 95% confidence you’d need a sample size of 27 or, for 90% confidence, a sample size of 19.
Summary and Discussion
We used estimates of unknown standard deviations for rating scales to create tables for sample size planning when researchers don’t have a prior estimate of the standard deviation of the items they plan to use.
Typical sample size requirements for binary metrics are two to four times as large as those required for rating scales. A major driver of this difference is the standard deviation of binary metrics. At its maximum value (p = .5), the standard deviation of binary metrics is 50% of the range of the binary scale (from 0 to 100%). Our estimate of typical standard deviations for individual multipoint items is about 25% of the maximum range.
The difference between sample size requirements for binary and rating scale data is greater when margins of error are smaller. The difference is notable but small in terms of the number of participants when margins of error are large. For example, a 24% margin of error with 90% confidence requires ten participants using the binary method, but only five for rating scales when the standard deviation is 25% of the scale’s range. The rating scale sample size is half of the binary metric sample size, but the difference in cost is just five participants. When the margin of error is small, however, there can be a large difference in the number of participants. For a 2% margin of error with 90% confidence, you need a sample of 1,689 participants using the binary method compared to 425 for typical rating scales—a difference of 1,264 participants.
The “right” sample size depends on the research details. If accurate estimates of binary metrics are a critical part of your research, use the sample sizes in the binary metrics column in Tables 2 and 3 because those sample sizes will also be more than adequate for your rating scale analyses. If your primary analyses will be rating scales, in most cases, you should use the “s = 25” column. If you have concerns that your standard deviations might be larger than average, use the “s = 28” column. If your primary analyses will be multi-item questionnaires, it’s reasonable to use the “s = 20” column.
We plan to follow up with guidance on sample sizes for rating scale comparisons. This article covered sample size estimation for confidence intervals. In the future, we will publish similar sample size tables for comparison of a sample with a specified benchmark and comparison of two sets of data for both within- and between-subjects experimental designs.


